Простые и сложные высказывания

Страница 1 из 5

Высказывание — более сложное образование, чем имя. При разложении высказываний на более простые части мы всегда получаем те или иные имена. Скажем, высказывание «Солнце есть звезда» включает в качестве своих частей имена «Солнце» и «звезда».

Высказывание — грамматически правильное предложение, взятое вместе с выражаемым им смыслом (содержанием) и являющееся истинным или ложным.

Понятие высказывания — одно из исходных, ключевых понятий логики.

Как таковое оно не допускает точного определения, в равной мере приложимого в разных ее разделах.

Высказывание считается истинным, если даваемое им описание соответствует реальной ситуации, и ложным — если не соответствует ей. «Истина » и «ложь» называются «истинностными значениями высказываний».

Из отдельных высказываний разными способами можно строить новые высказывания.

Например, из высказывания «Дует ветер» и «Идет дождь» можно образовать более сложные высказывания «Дует ветер, и идет дождь», «Либо дует ветер, либо идет дождь», «Если идет дождь, то дует ветер» и т. п.

Высказывание называется простым, если оно не включает других высказывании в качестве своих частей.

Высказывание называется сложным, если оно получено с помощью логических связок из других более простых высказываний.

Рассмотрим наиболее важные способы построения сложных высказываний.

Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами «не», «неверно, что». Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания «10 — четное число» является высказывание «10 не есть четное число» (или: «Неверно, что 10 есть четное число»).

Обозначим высказывания буквами А, В, С,… Полный смысл понятия отрицания высказывания задается условием: если высказывание А истинно, его отрицание ложно, и если А ложно, его отрицание истинно. Например, так как высказывание «1 есть целое положительное число» истинно, его отрицание «1 не является целым положительным числом» ложно, а так как «1 есть простое число» ложно, его отрицание «1 не есть простое число» истинно.

Простые и составные высказывания

Есть два вида высказываний: 1) простые и 2) составные, или сложные.

Под простым высказыванием будем понимать такое высказывание, которое не может быть разбито на более простые высказывания. Высказывания

А и В предыдущего примера – простые высказывания.

Про простое высказывание всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой.

Из простых высказываний при помощи так называемых логических связок или логических операций, например, союзов «и», «или», слов «если…, то…», «тогда и только тогда, когда…», можно строить сложные высказывания.

Например, из высказываний ; , используя логические операции, можно образовать следующие сложные высказывания:

 

,

 

,

 

 

.

 

Отметим, что сложные высказывания можно образовывать и из таких высказываний, которые не связаны между собой по смыслу. Например, высказывание:

 

{если слон – насекомое, то Антарктида покрыта тропическими лесами}

 

составлено при помощи логической операции «если…, то…» из двух высказываний, между которыми нет никакой смысловой связи.

Сложные высказывания, как и простые, всегда или только истинны, или только ложны. Истинность или ложность сложного высказывания полностью определяется, во-первых, тем, какие логические связки (операции) использованы для образования сложного высказывания. Во-вторых, истинность или ложность сложного высказывания определяется тем, какие из простых высказываний, образующих сложное высказывание, истинны, а какие – ложны.

 

 

Логические операции

Операции над высказываниями – логические операции – обычно задают в виде таблиц, называемых таблицами истинности.

Операция отрицания, или отрицание высказывания

Для каждого высказывания А может быть сформировано новое высказывание (читается «не А», или «не верно, что А») – это отрицание высказывания

А. Высказывание истинно, когда А – ложно, и ложно, когда А – истинно.

 

 

Таблица истинности для операции отрицания:

 

А

 

Операция отрицания – одноместная, или унарная, операция.

Последующие операции – двухместные, или бинарные.

Например, если — истинное высказывание, то

— ложное высказывание (отрицание А).

 

Отметим, что если {в комнате холодно}, то {в комнате не холодно}, но при этом высказывание {в комнате жарко} отрицанием высказывания

В не является.

 

Операция конъюнкции, или конъюнкция высказываний

Высказывание С, составленное из двух высказываний А и В при помощи союза «и», называют конъюнкцией (логическим произведением) этих высказываний: (выражение читается: «А и В»).

Логическое произведение истинно только в том случае, когда: «и А, и В одновременно истинны».

Таблица истинности для операции конъюнкции:

 

А	В

 

Пусть, например, , . Тогда высказывание С – истинно, т. к. истинно каждое из высказываний А и В, составляющих высказывание С.

Операцию конъюнкции можно определить и для нескольких высказываний, как связку высказываний, объединённых союзом «и». Конъюнкция из n высказываний – новое высказывание, причём высказывание

А = А_i ; где i = 1; 2; …; n

имеет значение «истина», если и А₁, и А₂, и … А_n одновременно истинны. Во всех других случаях эта конъюнкция имеет значение «ложь».

Пусть, например, А₁ , А₂ , А₃ , А₄ . Тогда высказывание

А₂ Ù А₃ Ù А₄ {(8 = 3) и (отец старше сына) и (Мурманск севернее Смоленска)} – ложное, в то время как высказывание

А₁ Ù А₃ Ù А₄ {(5 > 3) и

(отец старше сына) и (Мурманск севернее Смоленска)} – истинное.

 

 

Операция дизъюнкции, или дизъюнкция высказываний

Высказывание С, составленное из двух высказываний А, В при помощи союза «или», называют дизъюнкцией (логической суммой) этих высказываний: (выражение читается: «А или В»).

Сумма является истинным высказыванием тогда, когда, по крайней мере, одно из слагаемых истинно.

 

Таблица истинности для операции дизъюнкции:

 

А	В

 

Пусть, например, , . Тогда высказывание или – истинно, т.к. истинно каждое из высказываний А и В, составляющих высказывание С.

Операцию дизъюнкции можно определить и для нескольких высказываний как связку высказываний, объединённых союзом «или»:

А = А_i ; где i = 1; 2; …; n

В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.

 

Операция эквивалентности, или эквивалентность высказываний.

Высказывание С, составленное из двух высказываний А и В при помощи слов «тогда и только тогда, когда…», называют эквивалентностью высказываний А и В: .

Для эквивалентности используют знак (или ~).

Эквивалентность представляет собой истинное высказывание, когда: «высказывания и А, и В — оба истинны или оба ложны».

Таблица истинности для операции эквивалентности:

 

А	В

 

 

Пусть {число 3n является чётным}, {число n является чётным}.

Высказывание {число 3n является чётным тогда и только тогда, когда n – чётное число} есть эквивалентность высказываний А и В: .

Операция импликации, или импликация высказываний

Высказывание С, составленное из высказываний А и В при помощи слов «если…, то…», называют импликацией высказываний А и В и 1б1-начают

(выражение читается «из А следует В», или «если А, то В»).

Импликация ложна только в том случае, когда А – истинное высказывание, а В – ложное. Во всех других случаях импликация имеет значение «истина».

Таблица истинности для операции импликации:

 

А	В

 

Первый член импликации , – высказывание А, – называется посылкой, или условием, а второй член В – заключением.

Обратите внимание, что таблица истинности для импликации, в отличии от таблиц для конъюнкции, дизъюнкции и эквивалентности, изменяется при перестановке столбцов для А и В.

Отметим также, что импликация не полностью соответствует обычному пониманию слов «если…, то…» и «следует». Из третьей и четвёртой строк таблицы истинности для импликации вытекает, что если А – ложно, то, каково бы ни было В, высказывание считается истинным. Таким образом, из неверного утверждения следует (может следовать) всё, что угодно.

Например, утверждение «если 6 – простое число, то », или утверждение «если , то существуют ведьмы» являются истинными логическими утверждениями. Истинным является и рассмотренное ранее высказывание: «если слон – насекомое, то Антарктида покрыта тропическими лесами».

Как говорил Р. Декарт: «Если 2 х 2 = 5, то я докажу, что из трубы вылетает ведьма».

 

Для иллюстрации содержательного смысла импликации рассмотрим ещё один пример.

Пусть {папа завтра получит премию},

{папа завтра купит сыну велосипед}.

Импликация может быть сформулирована так:

«если папа завтра получит премию, то купит сыну велосипед».

Пусть А и В – истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием.

Если же папа, получив премию (А – истинно), не купит сыну велосипед (В – ложно), то это, можно сказать, – не логичный поступок, и импликация имеет значение «ложь».

Если папа не получит премию (А – ложно), но купит велосипед (В – истинно), то результат положителен (импликация истинна).

Наконец, в том случае, если, не получив премии (А – ложно), папа не купит велосипед (В – ложно), то обещание не нарушено, импликация истинна.

 

Задача 1. Даны два высказывания и . В чём заключаются высказывания , , , ? Какие из этих высказываний истинны и какие ложны?

Решение.

1) Высказывание , очевидно, ложно. Для того чтобы произведение двух высказываний было истинным, нужно чтобы оба высказывания были истинными.

2) Высказывание истинно, т.к. одно из слагаемых является истинным высказыванием.

Высказывание можно записать в виде одного верного нестрогого неравенства .

3) Эквивалентность ( тогда и только тогда, когда ) представляет собой ложное высказывание, т.к. А – ложно, а В – истинно.

4) Импликация то является истинным высказыванием.

В самом деле, импликация согласно определению ложна только тогда, когда А – истинно, а В – ложно.

 



А не подучить ли нам логику? — 8

1. Простые и сложные высказывания. Отрицание, конъюнкция, дизъюнкция

Высказывание – грамматически правильное предложение, взятое вместе с выражаемым им смыслом (содержанием) и являющееся истинным или ложным.

Высказывание – более сложное образование, чем имя. При разложении высказываний на части, мы всегда получаем те или иные имена. Скажем, высказывание «Солнце есть звезда» включает в качестве своих частей имена «Солнце» и «звезда».

Понятие высказывания – одно из ключевых в логике. Как таковое, оно не допускает точного определения, в равной мере приложимого в разных её разделах. Ясно, что всякое высказывание описывает определённую ситуацию, что-то утверждая или отрицая о ней, и является истинным или ложным.

Высказывание считается истинным, если даваемое им описание соответствует реальной ситуации, и ложным, если не соответствует ей. «Истина» и «ложь» называются истинностными значениями высказывания.

Из отдельных высказываний разными способами можно строить новые высказывания. Так, из высказываний «Дует ветер» и «Идёт дождь» можно образовать более сложные высказывания «Дует ветер и идёт дождь», «Либо дует ветер, либо идёт дождь», «Если идёт дождь, дует ветер» и т.п. Слова «и», «либо, либо», «если, то» и т.п., служащие для образования сложных высказываний, называются логическими связками.

Высказывание называется простым, если оно не включает других высказываний в качестве своих частей.

Высказывание является сложным, если оно получено с помощью логических связок из нескольких более простых высказываний.

Может показаться, что знакомство с высказываниями естественнее всего начать с изучения простых высказываний и их частей, и уже затем приступить к изучению того, как из простых высказываний образуются сложные.

В логике, однако, подход является обратным. Сначала рассматриваются способы построения сложных высказываний из более простых, при этом простое высказывание берётся как неразложимое далее целое (как «атом»), и только затем переходят к выявлению строения простых высказываний. Анализ структуры сложных высказываний предшествует анализу структуры простых.

Объясняется это следующим: для того, чтобы понимать способы сочетания высказываний, вовсе не обязательно знать, что такое простое высказывание; достаточно учитывать только то, что последнее имеет определённое значение истинности.

Простые высказывания чрезвычайно разнообразны, выявление составляющих их частей во многом зависит от принятого способа их анализа. Некоторые логические связи между высказываниями не зависят от строения простых высказываний. Разумно поэтому поступить так, как если бы мы знали все о простых высказываниях, т.е. оставить вопрос об их структуре на время в стороне и заняться логическими связями высказываний. Последняя задача является относительно лёгкой.

Та часть логики, в которой описываются логические связи высказываний, не зависящие от структуры простых высказываний, называется общей теорией дедукции.

Перейдём теперь к рассмотрению наиболее важных способов построения сложных высказываний.

Отрицание – логическая связка, с помощью которой из данного высказывания получается новое, причём, если исходное высказывание истинно, его отрицание будет ложным, и наоборот.

Отрицательное высказывание состоит из исходного высказывания и от

простые и сложные высказывания.логика

Отрицание, конъюнкция, дизъюнкция.

Наши рассуждения слагаются из высказываний. К примеру, в умозаключение «Некоторые птицы летают; значит, некоторые летающие — птицы» входят два разных высказывания.

Высказывание — более сложное образование, чем имя. При разложении высказываний на более простые части, мы всегда получаем те или иные имена. Скажем, высказывание «Солнце есть звезда» включает в качестве своих частей имена «Солнце» и «звезда».

Высказывание — грамматически правильное предложение, взятое вместе с выражаемым им смыслом (содержанием) и являющееся истинным или ложным.

Понятие высказывания — одно из исходных, ключевых понятий логики. Как таковое, оно не допускает точного определения, в равной мере приложимого в разных ее разделах. Ясно, что всякое высказывание описывает определенную ситуацию, что-то утверждая или отрицая о ней, и является истинным или ложным.

Высказывание считается истинным, если даваемое им описание соответствует реальной ситуации, и ложным, если не соответствует ей. «Истина» и «ложь» называются истинностными значениями высказывания.

Из отдельных высказываний разными способами можно строить новые высказывания. Так, из высказываний «Дует ветер» и «Идет дождь» можно образовать более сложные высказывания «Дует ветер и идет дождь», «Либо дует ветер, либо идет дождь», «Если идет дождь, дует ветер» и т. п. Выражения «и», «либо, либо», «если, то» и т. п., служащие для образования сложных высказываний, называются логическими связками.

Высказывание называется простым, если оно не включает других высказываний в качестве своих частей.

Высказывание является сложным, если оно получено с помощью логических связок из других, более простых высказываний.

Та часть логики, в которой описываются логические связи высказываний, не зависящие от структуры простых высказываний, называется общей теорией дедукции.

Отрицание — логическая связка, с помощью которой из данного высказывания получается новое высказывание, такое, что если исходное высказывание истинно, его отрицание является ложным, и наоборот. Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами «не», «неверно, что». Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания «10 — четное число» является высказывание «10 не есть четное число» (или: «Неверно, что 10 есть четное число»).

В результате соединения двух высказываний при помощи слова «и», мы получаем сложное высказывание, называемое конъюнкцией. Высказывания, соединяемые таким способом, называются членами конъюнкции. Например, если высказывания «Сегодня жарко» и «Вчера было холодно» соединить таким способом, получится конъюнкция «Сегодня жарко и вчера было холодно».

Конъюнкция истинна только в случае, когда оба входящих в нее высказывания являются истинными; если хотя бы один из ее членов ложен, то и вся конъюнкция ложна.

Определение конъюнкции, как и определения других логических связок, служащих для образования сложных высказываний, основывается на следующих двух предположениях:

каждое высказывание (как простое, так и сложное) имеет одно и только одно из двух значений истинности: оно является либо истинным, либо ложным;

истинностное значение сложного высказывания зависит только от истинностных значений входящих в него высказываний и способа их логической связи между собой.

Эти предположения кажутся простыми. Приняв их, нужно, однако, отбросить идею, что, наряду с истинными и ложными высказываниями, могут существовать также высказывания неопределенные с точки зрения своего истинностного значения (такие, как, скажем, «Через пять лет в это время будет идти дождь с громом» и т. п.). Нужно отказаться также от того, что истинностное значение сложного высказывания зависит также от «связи по смыслу» соединяемых высказываний.

В обычном языке два высказывания соединяются союзом «и», когда они связаны между собой по содержанию, или смыслу. Характер этой связи не вполне ясен, но понятно, что мы не рассматривали бы конъюнкцию «Он шел в пальто и я шел в университет» как выражение, имеющее смысл и способное быть истинным, или ложным. Хотя высказывания «2 — простое число» и «Москва — большой город» истинны, мы не склонны считать истинной также их конъюнкцию «2 — простое число и Москва — большой город», поскольку составляющие ее высказывания не связаны между собою по смыслу.

Упрощая значение конъюнкции и других логических связок и отказываясь для этого от неясного понятия «связь высказываний по смыслу», логика делает значение этих связок одновременно и более широким, и более ясным.

Соединяя два высказывания с помощью слова «или», мы получаем дизъюнкцию этих высказываний. Высказывания, образующие дизъюнкцию, называются членами дизъюнкции.

Слово «или» в повседневном языке имеет два разных смысла. Иногда оно означает «одно или другое или оба», а иногда «одно или другое, но не оба вместе». Высказывание «В этом сезоне я хочу пойти на «Пиковую даму» или на «Аиду» допускает возможность двукратного посещения оперы. В высказывании же «Он учится в Московском или в Ленинградском университете» подразумевается, что упоминаемый человек учится только в одном из этих университетов.

Первый смысл «или» называется неисключающим. Взятая в этом смысле дизъюнкция двух высказываний означает только, что по крайней мере одно из этих высказываний истинно, независимо от того, истинны они оба или нет. Взятая во втором, исключающем, смысле дизъюнкция двух высказываний утверждает, что одно из них истинно, а второе — ложно.

Символ V будет обозначать дизъюнкцию в неисключающем смысле, для дизъюнкции в исключающем смысле будет использоваться символ V . Таблицы для двух видов дизъюнкции показывают, что неисключающая дизъюнкция истинна, когда хотя бы одно из входящих в нее высказываний истинно, и ложна, только когда оба ее члена ложны; исключающая дизъюнкция истинна, когда истинным является только один из ее членов, и она ложна, когда оба ее члена истинны или оба ложны.

В логике и математике слово «или» всегда употребляется в неисключающем значении.

Разложение некоторого высказывания на простые, далее неразложимые части дает два вида выражений, называемых собственными и несобственными символами. Особенность собственных символов в том, что они имеют какое-то содержание, даже взятые сами по себе. К ним относятся имена (обозначающие некоторые объемы), нерешенные (отсылающие к какой-то области объектов), высказывания (описывающие какие-то ситуации и являющиеся истинными или ложными). Несобственные символы не имеют самостоятельного содержания, но в сочетании с одним или несколькими собственными символами образуют сложные выражения, уже имеющие самостоятельное содержание. К несобственным символам относятся, в частности, логические связки, используемые для образования сложных высказываний из простых: «… и …», «… или …», «либо …, либо …», «если …, то …», «… тогда и только тогда, когда …», «ни …, ни …», «не …, а …», «…, но не …», «неверно, что …» и т. п. Само по себе слово, скажем «или», не обозначает никакого объекта. Но в совокупности с двумя собственными, обозначающими символами это слово дает новый обозначающий символ: из двух высказываний «Письмо получено» и «Телеграмма отправлена» — новое высказывание «Письмо получено или телеграмма отправлена».

Центральная задача логики — отделение правильных схем рассуждения от неправильных и систематизация первых. Логическая правильность определяется логической формой. Для ее выявления нужно отвлечься от содержательных частей рассуждения (собственных символов) и сосредоточить внимание на несобственных символах, представляющих эту форму в чистом виде. Отсюда интерес формальной логики к таким, обычно не привлекающим внимания словам, как «и», «или», «если, то» и т. п.

Конспект «Логические значения, операции, выражения»

Логические значения, операции, выражения

Код ОГЭ: 1.3.3. Логические значения, операции, выражения

Алгебра логики, логические высказывания

Наука, изучающая формы, методы и законы правильного мышления, называется логикой. Она интересуется не содержанием мышления, а его формой, поэтому ее часто называют еще формальной логикой.

Форма мышления — это способ выражения мыслей или форма, по которой они строятся.

Форма, обозначающая какой–либо объект или отличающий его признак, называется понятием. Примеры понятий: «компьютер», «планета», «длина», «профессия».

Форма, утверждающая или отрицающая что–либо о свойствах понятий и отношений между ними, называется утверждением (высказыванием, суждением). Примеры логических утверждений: «Декодирование — процесс восстановления информации из закодированного представления»; «В двоичной системе используются две цифры: 0 и 1»; «Париж — столица Франции». Утверждения могут быть истинными или ложными. Так, высказывание «Шанхай — столица Франции» является ложным утверждением.

Форма, в которой из двух или нескольких высказываний получают новое утверждение, называется умозаключением. Пример умозаключения: «Периферийные устройства компьютера — это устройства для ввода или вывода информации. Сканер — устройство для переноса текста и изображений с бумаги в компьютер. Следовательно, сканер — периферийное устройство».

Правила, которые должны соблюдаться, чтобы на основании истинных суждений получить истинные выводы, — это законы мышления. Логика изучает эти законы и способы получения новых утверждений на основании уже имеющихся.

Математическая логика использует для установления истинности или ложности высказываний математические методы. Она пользуется специальным символьным языком, подобным языку математики, поэтому ее часто называют символьной логикой.

Алгебра логики — раздел математической логики, в котором методы алгебры используются в логических преобразованиях. Она изучает логические высказывания и методы установления их истинности или ложности с помощью алгебраических методов.

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно. Вопросительные и повелительные предложения не являются логическими высказываниями. Но и не каждое повествовательное предложение является логическим высказыванием. Например, суждение «Лето было очень дождливым» не является однозначным, для утверждения «Существует несколько Вселенных» нельзя однозначно определить истинность; поэтому такие предложения не являются логическими высказываниями (утверждениями).

Таким образом, отличительной особенностью логических высказываний является возможность принимать одно из двух значений — истина и ложь. Истинность или ложность высказывания определяется вне алгебры логики — с помощью наблюдений, научных исследований, практических опытов и т. п.

В алгебре логики различают простые высказывания и сложные (составные), составленные из нескольких простых. Если в высказывании нельзя выделить некую часть, которая не совпадает по смыслу с исходным высказыванием и сама является высказыванием, то оно называется простым высказыванием. Простые высказывания обычно обозначаются латинскими буквами A, B, C и т. д.

Сложные высказывания представляют собой объединение простых высказываний с помощью логических связок. В качестве логических связок используются слова «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний. Например, из простых высказываний «Офис фирмы находится в Мадриде» и «Офис фирмы находится в Берлине» можно составить сложные: «Офис фирмы находится в Мадриде или Берлине», «Офис фирмы находится в Мадриде и Берлине», «Если офис фирмы находится в Мадриде, то он находится в Берлине». Истинность первого из них означает, что офис фирмы находится в одном из названных городов или же имеются офисы в обоих городах. Ложность его означает, что ни в одном из этих городов офиса нет. Второе составное утверждение истинно тогда, когда в обоих городах имеется офис фирмы. Если же офис существует только в Берлине или только в Мадриде, — второе составное высказывание ложно.

В классической, двузначной алгебре логики логических значений всего два: истина (True) и ложь (False). Им соответствует цифровое представление — 1 и 0. Иногда эти значения записывают как «да» и «нет». Факт истинности или ложности некоторого высказывания А записывают соответственно как А = 1 или А = 0.

Логические операции

В алгебре логики логические связки рассматриваются как логические операции. Они имеют свои названия и обозначения. Результаты применения каждой операции к логическим высказываниям (истинным или ложным) можно представить в виде таблицы. В ней указывают все возможные сочетания значений исходных логических высказываний и истинность или ложность результата. Такие таблицы называют таблицами истинности операции. Обычно в них используют обозначения логических значений 0 и 1 или ложь и истина.

Основные логические операции — отрицание, конъюнкция, дизъюнкция, исключающая дизъюнкция, следование, эквивалентность.

Логическое отрицание (инверсия) — логическая операция, в результате которой из данного высказывания получается новое высказывание — отрицание исходного. Обозначается символически чертой сверху (Ā) или условными обозначениями ¬А, not А, не А (читается «отрицание А», «не А», «А ложно», «неверно, что А»).

Высказывание ¬А ложно, когда А истинно, и истинно, когда А ложно.

Таблица истинности операции отрицания

Если обозначить через А высказывание «Арбуз является ягодой», то ¬А соответствует высказыванию «Арбуз не является ягодой» («Неверно, что арбуз — ягода»).

Отрицание является унарной операцией. Унарная (одноместная) операция — это операция, которая применяется к одному операнду.

Остальные логические операции являются двуместными (бинарными). Бинарная (двуместная) операция — это операция, которая выполняется над двумя операндами.

Логическое умножение (конъюнкция) — операция, соединяющая два или более высказываний при помощи связки «и». Эта связка символически обозначается с помощью знака ∧ и читается «А и В». Для обозначения конъюнкции также применяются знаки: А • В, А & В, А и В, А and В, а иногда между высказываниями не ставится никакого знака: АВ.

Высказывание А ∧ В истинно только тогда, когда оба высказывания А и В истинны. Высказывание А ∧ В ложно только тогда, когда ложно хотя бы одно из высказываний А или В.

Таблица истинности операции конъюнкции

Например, высказывания «Лондон расположен севернее Лиссабона» и «Лондон расположен восточнее Лиссабона» истинны. Тогда истинным будет и составное логическое высказывание «Лондон расположен севернее и восточнее Лиссабона». Высказывания «Лондон расположен не севернее и восточнее Лиссабона», «Лондон расположен севернее и не восточнее Лиссабона», «Лондон расположен не севернее и не восточнее Лиссабона» — ложны.

Логическое сложение (дизъюнкция) — операция, соединяющая два или более высказываний при помощи связки « или». Эта связка символически обозначается с помощью знака v и читается «А или В». Для обозначения дизъюнкции также применяются знаки: А + В, А или В, А or В, А | B.

Высказывание А v В истинно только тогда, когда хотя бы одно из высказываний А или В истинно. Высказывание А v В ложно только тогда, когда оба высказывания А и В ложны.

Таблица истинности операции дизъюнкции

Например, высказывания «Виктор старше Ольги» и «Виктор — однофамилец Ольги» истинны. Тогда истинными будут и составные логические высказывания «Виктор старше Ольги или Виктор — однофамилец Ольги», «Виктор младше Ольги или Виктор — однофамилец Ольги», «Виктор старше Ольги или Виктор — не однофамилец Ольги». Высказывание «Виктор младше Ольги или Виктор — не однофамилец Ольги» — ложно, поскольку ложны оба составляющие его простые высказывания.

Исключающее сложение (исключающая дизъюнкция, строгая дизъюнкция, сложение по модулю два, дизъюнкция строго–разделительная) — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле (называется также исключающее «или»). Операция символически обозначается с помощью знака ⊕ и читается «либо А, либо В».

Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.

Таблица истинности операции строгой дизъюнкции

Например, результат исключающей дизъюнкции двух высказываний «Виктор не старше Ольги» и «Виктор младше Ольги» всегда будет истиной, кто бы из них не был старше.

Логическое следование (импликация) — логическая операция, соединяющая два высказывания при помощи связки «если… то» в сложное высказывание. Операция символически обозначается с помощью знака → и читается «Если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяются также знаки ⊃ или ⇒. Первое логическое высказывание является условием (посылкой), а второе — следствием (заключением).

Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина. Таким образом, импликация А → В ложна только тогда, когда А истинно, а В ложно (из истинного высказывания следует ложное). Во всех остальных случаях импликация истинна.

Таблица истинности операции импликации

Для высказываний «Луна — спутник Земли» и «Сумма углов треугольника не равна 180°» (первое истинно, второе ложно) составное высказывание «Если Луна — спутник Земли, то сумма углов треугольника не равна 180°» будет ложным. Однако истинными будут высказывания «Если Луна — спутник Земли, то сумма углов треугольника равна 180°», «Если Луна — не спутник Земли, то сумма углов треугольника не равна 180°» и «Если Луна — не спутник Земли, то сумма углов треугольника равна 180°». Этот пример наглядно демонстрирует, что в алгебре логики смысл высказываний не учитывается, а рассматриваются только их истинность или ложность.

Логическое равенство (эквивалентность, следование, двойная импликация, равнозначность) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В (читается «А эквивалентно B»). Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Для обозначения эквивалентности применяются знаки ~, ⇔.

Если оба высказывания имеют различные логические значения, результатом операции эквивалентности всегда будет ложь. Если же оба простые высказывания ложны или оба истинны, то составное логическое высказывание всегда будет истинно.

Таблица истинности операции эквивалентности

Для высказываний «Линейное уравнение всегда имеет решение» и «Кит — млекопитающее» их эквивалентность всегда будет истиной, так как оба простые утверждения истинны.

Таким образом, сводная таблица истинности для всех основных логических операций имеет вид:

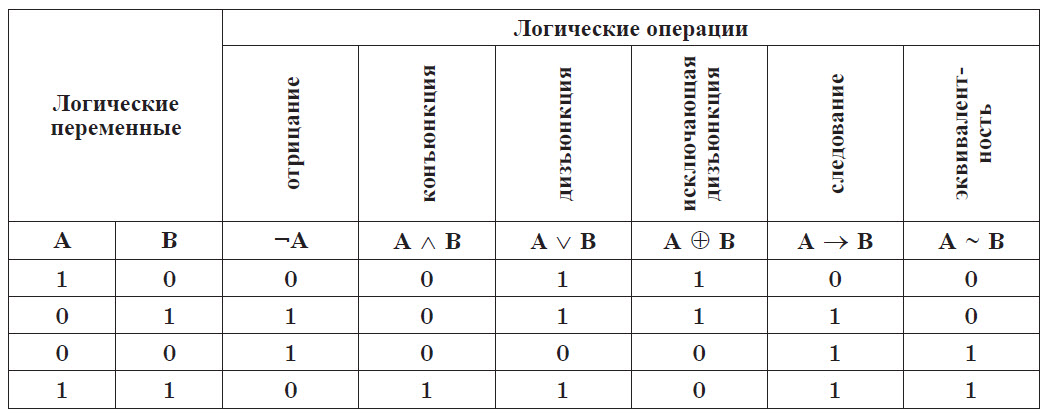
Логические выражения

Логические высказывания могут быть записаны в виде формул (логических выражений). Логические выражения включают логические переменные, знаки логических операций, логические константы (истина и ложь) и скобки. Логические выражения принимают значения истина или ложь.

Правила построения логических выражений:

• любая логическая переменная или константа (истина и ложь) являются логическим выражением;
• если А — , то ¬А — тоже логическое выражение;
• если А и В — логические выражения, то А ∧ В; А v В ; А ⊕ В; А → В; А ~ В — тоже логические выражения.

Например, A ⊕ истина v В v ложь — логическое выражение; А v ⊕ В v ложь не является логическим выражением.

Логическое выражение, принимающее значение истина при любых значениях входящих в него переменных, называется тождественно–истинным выражением (тавтологией). Например, А v В v ¬А; (А ∧ ¬А) → В.

Логическое выражение, принимающее значение ложь при любых значениях входящих в него переменных, называется тождественно–ложным выражением (противоречием). Например, А ∧ ¬А; В ~ ¬В.

Логическое выражение, принимающее как значение ложь, так и значение истина при разных значениях входящих в него переменных, называется выполнимым выражением.

ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Для сложных логических выражений, содержащих несколько логических операций, определен порядок выполнения действий (приоритет): сначала операции отрицания, затем операции логического умножения, потом операции логического сложения и исключающего сложения, последними выполняются операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения может быть изменен с помощью скобок.

Приоритет выполнения логических операций в логических выражениях

Пример 1
Определить порядок выполнения логических операций в выражении.
Вычислить его значение, если А = 1, В = 0, С = 1.
¬А ∧ С v (A ⊕ В) ∧ В

Решение. Первыми вычисляются значения в скобках. Затем выполняются операции по приоритетам: самый высокий приоритет имеет операция отрицания, после нее, как в математике, следуют операции умножения, а затем сложения. Таким образом, порядок будет следующий: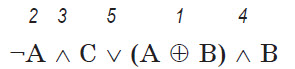

Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Итог: 0.
Ответ: логическое выражение ложно.

Пример 2
Для каких из приведенных слов истинно следующее высказывание?
(Вторая буква гласная) ИЛИ (Первая буква гласная) И НЕ (Длина имени не больше 5 букв)

1) Олег   2) Марианна  3) Светлана   4) Ольга.

Решение.

1.  В соответствии с приоритетом выполнения операций сначала нужно вычислить результат операции отрицания: «Длина имени больше 5 букв». Такие имена — Марианна, Светлана.
2. Затем необходимо рассчитать результат конъюнкции (связка И) второго и третьего высказываний. Конъюнкция истинна только тогда, когда истинны оба высказывания. Следовательно, нужно выбрать имена, в которых и первая буква гласная, и длина имени больше 5 букв — таких имен среди вариантов нет.
3. Результат дизъюнкции (связка ИЛИ) истинен только тогда, когда истинно или одно, или второе, или одновременно оба простые высказывания. Первое простое высказывание истинно для имени Марианна, второе ложно для указанных имен. Таким образом, верный вариант ответа — 2.

Ответ: 2) Марианна.

СВЯЗЬ МЕЖДУ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ

Между логическими операциями существует взаимосвязь. Операции исключающего «или», следования и эквивалентности можно выразить через операции отрицания, логического сложения и умножения, что отражено в следующей таблице.

Связь между логическими операциями

 

Поэтому операции отрицания, логического сложения и логического умножения называют основными логическими операциями: их достаточно, чтобы построить любое логическое выражение.

Если логическое выражение содержит только операции отрицания, логического сложения и логического умножения, говорят, что выражение находится в нормальной форме.

РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ

Логические выражения, значения которых совпадают для всех наборов входящих в них переменных, называются равносильными, или эквивалентными.

Чтобы убедиться, что два выражения равносильны, можно построить для них таблицы истинности. Если в таблицах совпадут все значения, значит, выражения равносильны.

Пример 3
Проверить равносильность выражений А ~ E и (Ā ∧ Ē) v (A ∧ E).

Решение. Для проверки следует создать таблицу истинности, содержащую столько строк, сколько возможно наборов значений переменных, входящих в выражение. Для двух переменных (А и E) количество наборов равно четырем. К двум столбцам для значений переменных (А и E) нужно присовокупить количество столбцов, равное количеству операций в выражении. Таким образом, необходимо создать таблицу, содержащую 4 строки и 7 столбцов.

Заполним первые 2 столбца (А и E) всеми сочетаниями значений переменных. Запишем в качестве заголовков столбцов все операции выражения в порядке их выполнения (в соответствии с приоритетами и скобками). Рассчитаем значения этих операций: сначала выражения в скобках, затем результат их сложения.

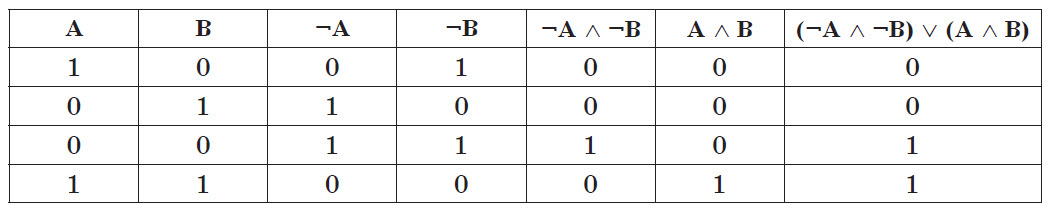
Последний столбец содержит результирующее значение выражения. Он совпадает с таблицей истинности для операции эквивалентности. Следовательно, выражения равносильны.

Основные законы алгебры логики

Для сложных логических выражений с большим числом переменных определение их истинности путем построения таблиц истинности становится громоздким. В таких случаях применяют способы упрощения выражений. Под упрощением понимают равносильное преобразование выражения к его нормальной форме.

Нормальная форма выражения содержит только операции отрицания, конъюнкции и дизъюнкции и не содержит отрицания выражений и двойных отрицаний.

Для упрощения используют равносильные преобразования, которые иначе называют основными законами алгебры логики.

Тождественные преобразования логических выражений

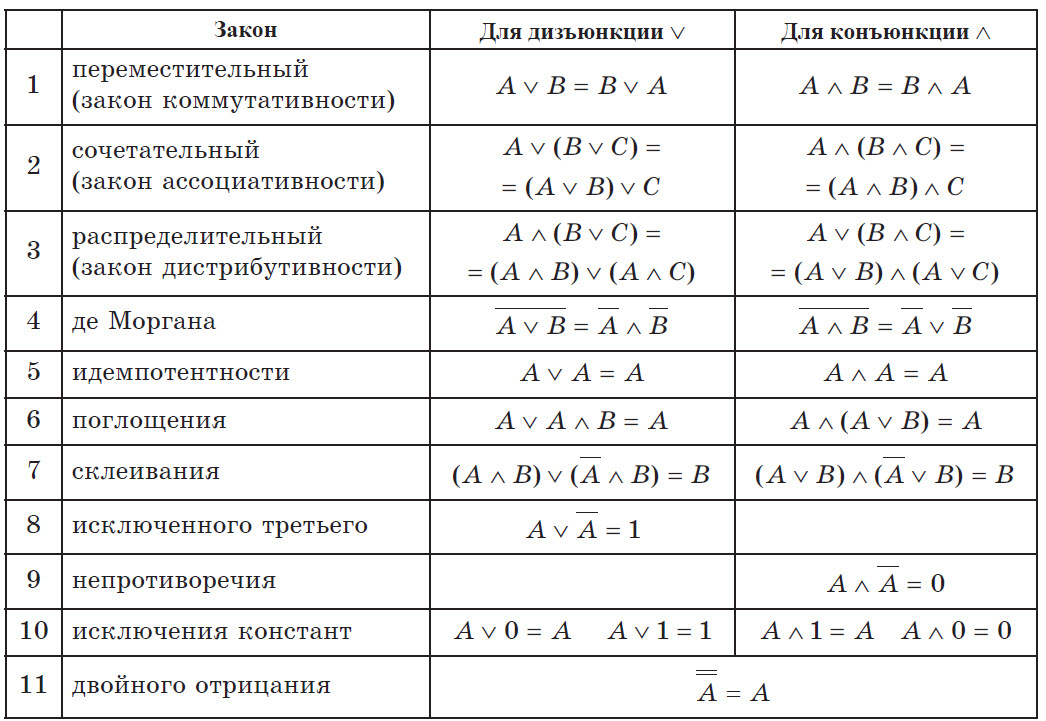
Для всех тождественных преобразований выполняется закон двойственности: если в формуле преобразования заменить конъюнкцию на дизъюнкцию, дизъюнкцию — на конъюнкцию, значения 1 — на 0, 0 — на 1, то закон, сформулированный для конъюнкции, примет форму аналогичного закона для дизъюнкции, и наоборот.

Прежде всего при равносильных преобразованиях избавляются от отрицания выражений, потом — от логических операций исключающей дизъюнкции, следования и эквивалентности. Затем используют законы алгебры логики для уменьшения количества переменных в выражении.

Пример 4
Выбрать выражение, которое равносильно выражению (A ∧ B) v (Ā ∧ B).

1) A         2) A ∧ B          3) Ā ∧ B           4) B

Решение. В соответствии с законом склеивания (A ∧ B) v (Ā ∧ B) = B, следовательно, исходное выражение равносильно выражению В.
Ответ: 4) В.

ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ

Выражения, которые принимают логические значения (истина или ложь) в результате выполнения операций сравнения (больше >, меньше <, больше или равно ≥, меньше или равно ≤, равно =, не равно ≠), также являются логическими выражениями. Кроме операций сравнения и логических операций такие выражения могут включать функции и алгебраические операции. Приоритет выполнения этих операций таков:

1. Вычисление значений функций.
2. Выполнение алгебраических операций (вначале возведение в степень, затем умножение и деление, после чего вычитание и сложение).
3. Выполнение операций сравнения (в порядке записи).
4. Выполнение логических операций (сначала операции отрицания, затем операции логического умножения, потом операции логического сложения, последними выполняются операции импликации и эквивалентности).

Если в логическом выражении используются скобки, то сначала выполняются заключенные в них операции.

Пример 5
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1          2) 2         3) 3        4) 4

Решение. В соответствии с приоритетами операций сначала следует выполнить операции сравнения, затем отрицания, а потом — конъюнкцию. Отрицанием высказывания М ≥ 10 является высказывание М < 10. Получим выражение М < 10 ∧ M > 3. Для того чтобы это выражение (конъюнкция) было истинным, должны выполняться (т. е. быть истинными) оба неравенства. Следовательно, значение М должно быть больше 3, но меньше 10. Среди предложенных значений этому условию удовлетворяет только одно — число 4.
Ответ: 4) 4.

Задачи, подобные предыдущему примеру, можно решать и с помощью таблиц истинности.

Пример 6.
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1           2) 2         3) 3        4) 4

Решение. Составим таблицу истинности: все операции выражения укажем в столбцах таблицы, все предложенные значения М укажем в ее строках. Рассчитаем значения таблицы:

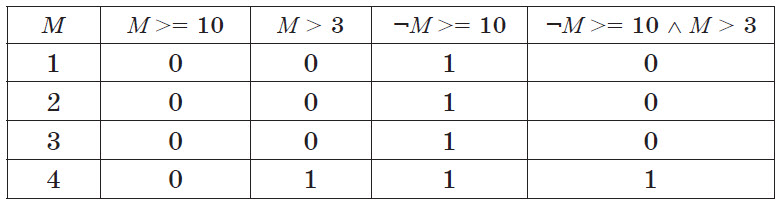
Последний столбец содержит результат всего выражения. Истинным оно будет только для значения числа М, равного 4.
Ответ: 4) 4.

Пример 7.
В табличной форме представлены ежемесячные данные о продаже групп товаров за полгода. Сколько групп товаров демонстрировали рост продаж в весенние месяцы или вышли на уровень свыше 80 % в июне?

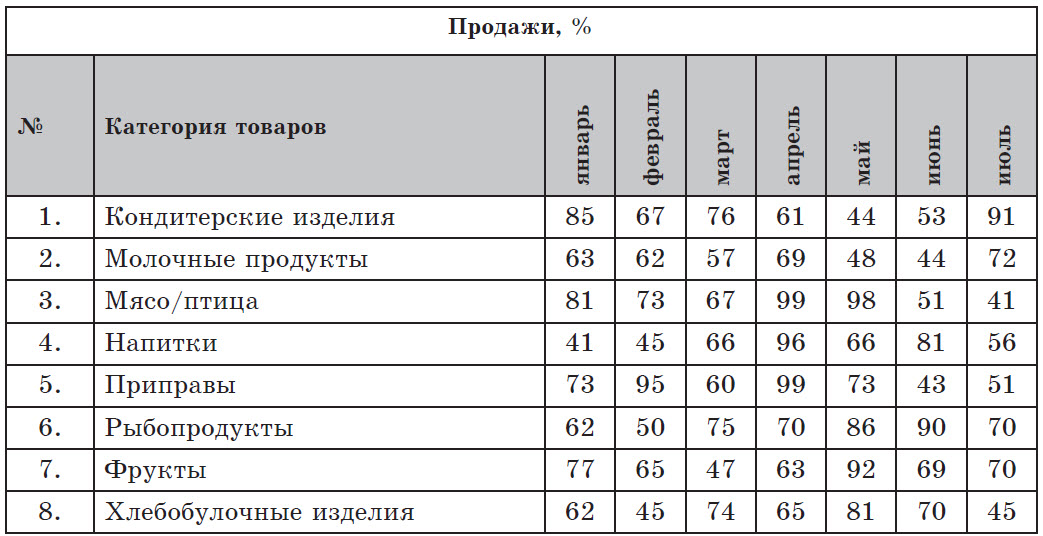
Решение. Переформулируем условие задачи: необходимо найти группы товаров, для которых (Март < Апрель) ∧ (Апрель < Май) v (Июнь > 80).

Введем обозначения:
А = (Март < Апрель)
В = (Апрель < Май)
С = (Июнь > 80)

Тогда выражение можно записать как А ∧ В v С.

Логическое выражение состоит из одной конъюнкции и одной дизъюнкции. Значение выражения конъюнкции истинно только тогда, когда истинны оба составляющие его простых выражения ((Март < Апрель) и (Апрель < Май)). Значение выражения дизъюнкции будет истинным, если хотя бы одно из составляющих его простых высказываний будет истинным.

Составим таблицу истинности для исходных данных.

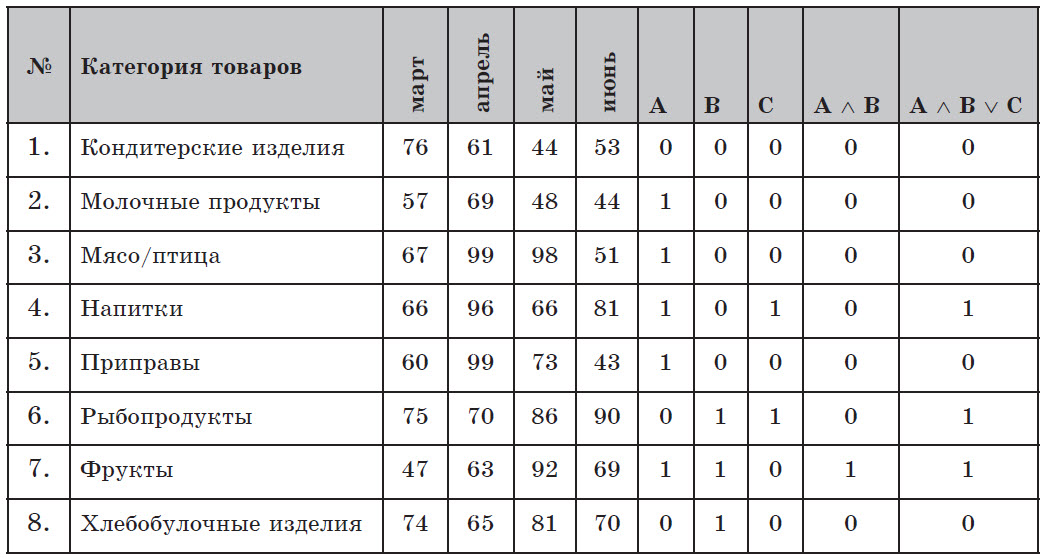
Логическому выражению удовлетворяют 3 записи — 4–я, 6–я и 7–я.
Ответ: 3.

 

---

Конспект урока по информатике «Логические значения, операции, выражения».

Вернуться к Списку конспектов по информатике.

 

сложное высказывание — это… Что такое сложное высказывание?



сложное высказывание

высказывание, полученное с помощью логических связок из простых высказываний. Наиболее употребительны С. в., образованные с помощью слов: «и», «или», «если, то», «если и только если», «не». Вместо этих слов в логике используются символы: &, v, -&GT;, ?, сложное высказывание. С. в. А& В называется конъюнкцией («А и В»), A v В — дизъюнкцией («А или В»), А — В — импликацией («Если A, то В»), А = В — эквивалентностью («А, если и только если В»), сложное высказывание А — отрицанием («Неверно, что A», или «не-A»).

Установление смысла и способа употребления логических связок, позволяющих образовывать С. в., является задачей наиболее фундаментальной и вместе с тем самой простой части логики — исчисления высказываний.

Словарь по логике. — М.: Туманит, изд. центр ВЛАДОС. А.А.Ивин, А.Л.Никифоров. 1997.

• следствие
• случайность логическая

Смотреть что такое «сложное высказывание» в других словарях:

• высказывание контрфактическое — (от лат. contra против, factum событие) сложное высказывание, в котором с помощью союза если бы…, то бы… объединяются два высказывания A и В. В естественном языке ему соответствуют предложения, имеющие форму условно сослагательного наклонения …   Словарь терминов логики

• Высказывание (Предложение) Контрфактическое — (от лат. contra против, factum событие) а сложное высказывание, в котором с помощью союза лесли бы…, то бы …   Словарь терминов логики

• ВЫСКАЗЫВАНИЕ — грамматически правильное повествовательное предложение, взятое вместе с выражаемым им смыслом. В логике употребляется несколько понятий В., существенно различающихся между собой. Прежде всего это понятие дескриптивного, или о п и с а тельного,… …   Философская энциклопедия

• Сложное синтаксическое целое (сверхфразовое единство, микротекст, период) — группа тесно взаимосвязанных законченных предложений, объединенных общностью темы в смысловой блок. Смысловые отношения, объединяющие самостоятельные предложения в С. с. ц., подкрепляются различными средствами: лексическими (повторение в… …   Педагогическое речеведение

• условное высказывание — сложное высказывание, формулируемое обычно с помощью связки если…, то… и устанавливающее, что одно событие, состояние и т. п. является в том или ином смысле основанием или условием другого. Напр.: Если есть огонь, то есть дым , Если число… …   Словарь терминов логики

• логика высказываний — (Пропозициональная логика) раздел логики, формализующий употребление логических связок и , или , не , если, то и т. п., служащих для образования сложных высказываний из простых. Высказывание называется простым, если оно не включает в себя другие… …   Словарь терминов логики

• таблица истинности — таблица, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний. В классической математической логике предполагается, что каждое простое (не содержащее логических… …   Словарь терминов логики

• ИМПЛИКАЦИЯ — [лат. implicatio сплетение, переплетение] лог. логическая операция, образующая сложное высказывание из двух высказываний посредством логической связки, соответствующей союзу «если… то…». Словарь иностранных слов. Комлев Н.Г., 2006. импликация …   Словарь иностранных слов русского языка

• ИМПЛИКАЦИЯ — (от лат. implicatio сплетение, от implico тесно связываю) логическая связка, соответствующая грамматической конструкции «если.., то…», с помощью которой из двух простых высказываний образуется сложное высказывание. В импликативном высказывании… …   Философская энциклопедия

• Троичные функции — Троичной функцией в теории функциональных систем и троичной логике называют функцию типа , где   троичное множество, а   неотрицательное целое число, которое называют арностью или местностью функции. Элементы множества  цифровые… …   Википедия

Книги

• Текст. Его единицы и глобальные категории, А. Ф. Папина. В учебнике называются единицы текста: сложное синтаксическое целое (ССЦ), дискурс, высказывание, предложение. Показано их актуальное членение. Характеризуются коммуникативные функции… Подробнее  Купить за 611 руб
• Текст: его единицы и глобальные категории, Папина А.Ф.. В учебнике называются единицы текста: сложное синтаксическое целое (ССЦ), дискурс, высказывание, предложение. Показано их актуальное членение. Характеризуются коммуникативные функции… Подробнее  Купить за 593 грн (только Украина)
• Сборник диктантов и упражнений по пунктуации. Словосочетание, простое предложение, сложное…, Попова Татьяна Анатольевна. Эта книга является второй из серии методических пособий по развитию орфографической, пунктуационной грамотности и культуры речи. В сборнике представлены различные упражнения и диктанты,… Подробнее  Купить за 85 руб

Другие книги по запросу «сложное высказывание» >>

javascript — Разница между простым и сложным утверждением

Переполнение стека

1. Около
2. Продукты
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. Реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

Загрузка…

2. Авторизоваться зарегистрироваться

3. текущее сообщество

.

Что такое простые, сложные и сложные предложения?

Одна вещь, на которую ProWritingAid отлично подчеркивает, — это разнообразие длин предложений, которые вы используете при написании. Вы знаете, что изменение длины создает более лирический изгиб вашего письма. Вам не нужны короткие предложения. Также вам не нужны длинные предложения, которые усложняют понимание вашего читателя.

Простые, составные и сложные предложения — все способы варьировать длину. Посмотрим, как они работают.

Простые предложения

В простом предложении есть только самые элементарные строительные блоки предложения: подлежащее и глагол, используемые в законченной мысли, также называемой независимым предложением.

Вот несколько примеров простых предложений:

• Кристина пила утренний кофе. ( Кристина = предмет , выпила = глагол )

• Кристина приняла душ и оделась. ( Кристина = испытуемых , мылась и одела = составные глаголы )

Простые предложения обычно короткие.Вы можете использовать сложные подлежащие и глаголы, чтобы увеличить длину, но по большей части использование слишком большого количества простых предложений делает ваше письмо прерывистым.

Сложные приговоры

Сложные предложения объединяют два независимых предложения вместе с союзом.

• Кристина выпила утренний кофе, затем приняла душ и оделась.

Обратите внимание, что первая часть предложения и последняя часть могут стоять отдельно как независимые предложения. Главное — не использовать слишком много сложных предложений вместе, иначе ваше письмо будет звучать неестественно.

Сложные предложения

В сложном предложении используется независимое предложение в сочетании с одним или несколькими зависимыми предложениями. Зависимое предложение похоже на независимое предложение, но оно не может стоять само по себе как законченное предложение. В сложных предложениях также используются союзы, чтобы связать их вместе.

Примеры:

• Кристина опоздала на утренний поезд, так как она проснулась поздно, когда сработал ее будильник.

• Наблюдая за отходом поезда от станции, Кристина поняла, что снова опоздает на работу.

Зависимые предложения также могут находиться в конце независимого предложения, как в этих примерах:

• Кристина опоздала на утренний поезд, потому что проснулась поздно, когда сработал ее будильник.

• Кристина поняла, что снова опоздает на работу, когда смотрела, как поезд отходит от станции.

Вот сложное предложение с двумя составными независимыми предложениями и одним зависимым предложением:

• Кристина опоздала на свой утренний поезд и, наблюдая, как он отходит от станции, поняла, что снова опоздает на работу.

Заинтересованы в других статьях из нашей серии «Гимназия»?

---

Поднимите свое письмо на новый уровень:

20 советов по редактированию от профессиональных писателей

Пишете ли вы роман, эссе, статью или электронное письмо, хорошее письмо является неотъемлемой частью передачи ваших идей.

Это руководство содержит 20 наиболее важных советов и приемов письма от широкого круга профессиональных писателей.

Подпишитесь на написание хаков, специальных предложений и бесплатных вещей

Мы не передадим ваши данные

Вы уже пробовали ProWritingAid? Чего же ты ждешь? Это лучший инструмент для обеспечения надежности, четкости и отсутствия ошибок в вашей копии!

ProWritingAid: гуру грамматики, редактор стилей и наставник в одном пакете.

У самых успешных людей в мире есть тренеры. Независимо от вашего уровня письма, ProWritingAid поможет вам достичь новых высот. Отличное письмо зависит от гораздо большего, чем просто правильная грамматика. Вам нужен инструмент для редактирования, который также выделяет проблемы стиля и сравнивает ваши произведения с лучшими писателями в вашем жанре. ProWritingAid поможет вам найти лучший способ выразить свои идеи.

.

Простые составные и сложные предложения

В этом разделе мы обсудим простые составные и сложные предложения в грамматике английского языка. Основываясь на структуре предложений, мы классифицируем предложения на 3 широкие категории:

Простые предложения

Простое предложение — это предложение, в котором есть только одно подлежащее и одно предикат, или простое предложение — это предложение, содержащее только один конечный глагол.

Пример:

1. Честного человека любят все.
   Тема: честный человек
   Предикат: все любят
2. Все мы вернулись домой.
   Тема: все мы
   Предикат: вернулся домой

Составные предложения

Составное предложение — это предложение, состоящее из двух или более координационных предложений, соединенных согласующим союзом.

Пример:

1. Она идет в магазин, или она идет в торговый центр.
   Пункт 1: Она идет в магазин.
   Пункт 2: Она идет в торговый центр.
   Соединение: или
2. Взошло солнце, и все выглядело ярким и блестящим.
   Пункт 1: Солнце взошло.
   Пункт 2: Все выглядело ярко.
   Соединение: и

Координационная статья

Координационная статья — это одна из двух или более статей, которые являются независимыми или равными. На основе координационного союза, используемого в составном предложении, оно может быть 4 типов:

Совокупные приговоры

В этом типе составного предложения одно предложение просто добавляется к другому.

1. Хасан пел, а я танцевал.
2. Путь был долгим, а ночь была холодной.
3. Она не может ни говорить, ни писать.

Альтернативные предложения

В этом типе составного приговора предлагается альтернатива или выбор между одним утверждением и другим.

1. Она должна работать, иначе она умрет.
2. Либо он дурак, либо он сумасшедший.
3. Идите быстро, иначе вы пропустите автобус.

Оговорки

В этом типе составного приговора одно утверждение или факт противопоставляется или противопоставляется другому.

1. Он медлителен, но устойчив.
2. Он беден, но счастлив.
3. Мудрые любят истину, а глупцы ее избегают.

Иллюзорные приговоры

В этом типе составного предложения одно предложение указывает причину, а другое подразумевает следствие этой причины.

1. Он не учился, поэтому и проиграл.
2. Я болею, поэтому сегодня не могу присутствовать на собрании.
3. Однажды он умрет, потому что все люди смертны.

В зависимости от количества координирующих положений составное предложение может быть:

1. Двойное предложение (2 координирующих предложения)
2. Множественное предложение (более 2 координирующих предложений)

Сложные предложения

Сложное предложение — это предложение, состоящее из одного основного предложения (независимое предложение) и одного или нескольких подчиненных предложений (зависимое предложение).

Пример

1. Я сжег обед, но не торт.
   Основная статья: Я сжег обед.
   Второстепенное предложение: Но не торт.
2. Хотя он был очень богат, он все же был несчастен.
   Основная статья: Он все еще был недоволен.
   Дополнительная статья: Хотя он был очень богат.

Основная статья

Основная или основная статья — это независимая статья, которая может действовать сама по себе.

Дополнительная оговорка

Полное значение подчиненного предложения зависит от главного предложения.

.

Структура предложения на английском языке: простые, составные, сложные и составно-сложные предложения

В то время как цель предложения относится к функции предложений, структура предложения относится к структуре или форме предложений на языке. В английском языке существует четыре типа структур предложений: простые предложения, составные предложения, сложные предложения и составно-сложные предложения.

Простые предложения

Первый тип предложения в английском языке — это простое предложение.Простое предложение состоит из одного глагольного предложения. Глагольные предложения — это независимые предложения, которые состоят из подлежащего и сказуемого. Некоторые грамматики ссылаются на предложения глагола как на главные, матричные или вышестоящие.

• Тема | Предикат
  Она | смеялись.
  Пожарная сигнализация | звучало громко.
  Странная девушка | посещает библиотеку с отцом.
  Сорок две тысячи ондатр и один одинокий вол | замышляли разрушить город.

Составные предложения

Второй тип предложения в английском языке — составное предложение.Составное предложение состоит из двух или более глагольных предложений, соединенных (1) координирующим союзом или (2) парой корреляционно-координирующего союза. Например, следующие предложения являются составными предложениями:

• Глагол Предложения | Координационное соединение | Глагол Статья
  Она любила океан, | пока | она никогда не ходила к морю.
  Мальчики собрали гамбургеры, | и | девушки выбрали бутерброды с курицей.
  Он надеялся купить новую машину, | так | он скопил все свои деньги.
  Учитель разрешил записи во время теста, | но | все студенты все равно проиграли.
• Корреляционная связь | Предложение глагола | Координационное соединение | Глагол Предложение
  Оба | ручей затопил мост, | и | упавший ручей преградил дорогу.
  Либо | он прекращает свое грубое поведение, | или | Я ухожу с ужина рано.
  Либо | новостная станция испытывает технические трудности, | или | происходят действительно странные события.
  Ни то, ни другое | посылка прибыла вовремя, | ни | компания получила счет за доставку.

Сложные предложения

Третий тип предложений в английском языке — сложное предложение.Сложное предложение состоит из одного придаточного глагола и одного или нескольких придаточных предложений, включая придаточные предложения существительного, прилагательного и наречия. Предложения существительного — это придаточные предложения, которые состоят из подчиненного союза, известного как маркер предложения существительного, за которым следует предложение, и которые выполняют номинальные функции. Прилагательные придаточные предложения — это придаточные предложения, которые состоят из подчинительного союза, известного как относительное местоимение, за которым следует придаточное слово, и которые выполняют функции прилагательного. Предложения наречия — это придаточные предложения, которые состоят из подчиняющего союза, за которым следует предложение, и которые выполняют наречие функции.Например, следующие предложения являются сложными предложениями:

• Предложение существительного | Глагольная фраза
  Что музей закрыт | удивил меня.
• Существительное Фраза | Прилагательное Прилагательное | Глагол Фраза
  Птица | упал с линии электропередачи | пережил травмы.
• Предложение наречия | Глагольный пункт
  После того, как я безумно бросился к своей машине, | дождь начал утихать.
  Если он рано на вечеринку, | хозяйка бросится на стол в абажуре.
• Глагольное предложение | Статья наречия
  Она провалила первый семестр занятий | потому что она слишком много веселилась и слишком мало училась.
  Женщина в футбольной майке | хотя ей не нравился этот спорт.
• Предложение наречия | Предложение глагола | Наречие Clause
  Хотя она плохо себя чувствовала, | девочка отказалась извиняться | потому что она была влюблена в маленького мальчика.
  Пока его отец работал над грузовиком, | молодой человек тщательно записывал | чтобы он не пропустил важный шаг в процессе.

Составно-сложные предложения

Четвертый тип предложений в английском языке — составно-сложные предложения.Составно-сложное предложение состоит из двух или более предложений глагола и одного или нескольких предложений существительного, прилагательных и наречий. Другими словами, составные сложные предложения представляют собой комбинации одного или нескольких составных предложений и одного или нескольких сложных предложений. Например, следующие предложения являются составно-сложными предложениями:

• Прилагаемое существительное | Глагольная фраза | Соединение | Глагол Статья
  О том, что музей закрыт | удивил меня, | но | мою маму эта новость не беспокоила.
• Глагольное предложение | Предложение наречия | Соединение | Глагол Статья
  Она работала в библиотеке | с тех пор, как она закончила, | но | она надеялась найти новую работу.
• Предложение наречия | Предложение глагола | Соединение | Глагол Clause
  Хотя он любил меняющиеся листья, | он никогда не ездил в Новую Англию осенью, | так | он решил заказать поездку на сентябрь следующего года.
• Глагольное предложение | Предложение наречия | Соединение | Предложение глагола | Наречие Статья
  Папа косил газон | хотя у него аллергия на траву, | и | Мама испекла банановый хлеб | хотя она ненавидит запах бананов.

Другой анализ придаточных предложений существительных и прилагательных

Различные грамматики по-разному анализируют предложения, содержащие придаточные предложения существительного и прилагательное или относительное предложение.Одно из определений сложного предложения — это предложение, которое содержит предложение глагола и зависимое или придаточное предложение. Помимо предложений наречий, предложения существительного и прилагательного являются зависимыми предложениями. Согласно этому определению, следующие предложения анализируются как сложные предложения:

• То, что она провалила уроки рисования , меня серьезно удивило. (предложение существительного)
• Его родители подарили , что он хотел компьютер на день рождения , подумал.(существительное)
• Женщина , которой вы доставили цветы , принимает окончательное решение о найме. (прилагательное)
• Чтение, , одно из моих любимых занятий , стимулирует ум. (прилагательное)

Согласно второму определению сложного предложения — предложение, которое состоит из одного предложения глагола и одного или нескольких предложений наречий — предложения, которые состоят из одного предложения глагола, содержащего предложения существительного или прилагательного (или оба ) — простые предложения.Например, более ограниченное определение анализирует предыдущие предложения как простые предложения.

Почему некоторые грамматики не включают придаточные предложения существительных и прилагательных в определение сложного предложения? В отличие от предложений наречий, многие предложения существительных и прилагательных нельзя удалить из предложения без изменения грамматики предложения глагола. Например, в первом предложении — То, что она провалила свой художественный класс , меня серьезно удивило — предложение существительного То, что она провалила свой художественный класс , функционирует как подлежащее глагольного предложения.Без предложения существительного в предложении глагола отсутствует подлежащее. Таким образом, существительное и прилагательное являются составными частями глагольного предложения. Однако предложения наречий никогда не являются составными частями предложения глагола и могут быть удалены без изменения грамматики предложения глагола. Таким образом, совокупность предложений существительного и прилагательного по сравнению с предложениями наречий определяет мое определение сложного предложения как предложения, которое состоит из одного предложения глагола и одного или нескольких предложений наречий. Предложение, состоящее из единственного глагольного предложения с или без существительного или прилагательного, является простым предложением независимо от каких-либо существительных или прилагательных, встроенных в грамматическую структуру глагольного предложения.Однако в большинстве грамматик сложное предложение определяется как состоящее из глагольной фразы и по крайней мере одного придаточного предложения.

Четыре типа структур предложений в английском языке — это простые предложения, составные предложения, сложные предложения и составные сложные предложения.

Резюме

Четыре типа структур предложений в английском языке — это простые предложения, составные предложения, сложные предложения и составные сложные предложения.

Простые предложения состоят из одного глагольного предложения.

Составные предложения состоят из двух или более глагольных предложений, соединенных (1) координирующим союзом или (2) парой корреляционно-координирующего союза.

Сложные предложения состоят из одного глагольного предложения и одного или нескольких придаточных предложений.

Сложно-сложные предложения состоят из двух или более глагольных предложений и одного или нескольких придаточных предложений.

Список литературы

Brinton, Laurel J.И Донна М. Бринтон. 2010. Лингвистическая структура современного английского языка , 2-е изд. Амстердам: Издательство Джона Бенджаминса.
Hopper, Paul J. 1999. Краткий курс грамматики . Нью-Йорк: W. W. Norton & Company.
Хаддлстон, Родни. 1984. Введение в грамматику английского языка . Кембридж: Издательство Кембриджского университета.

.