Ментальная арифметика для детей от 5 до 16 лет • Детский клуб «Классики»

Вы сможете решить этот пример за несколько секунд, без помощи калькулятора?

872+116-761+262-378=?

А ваш ребенок сможет.

Детский клуб «Классики» открывает новое направление – Ментальная Арифметика для детей от 5 до 16 лет.

Что такое ментальная арифметика?

• Ментальная – значит «мысленная». Ментальная арифметика – вычисления в уме, без помощи калькулятора, тетрадок и других вспомогательных средств
• Ментальная арифметика зародилась в древнем Китае, а в 21 веке приобрела фантастическую популярность. Завоевав азиатские страны, ментальная арифметика быстро развивается в Европе и Америке. Сейчас во всем мире работает более 5000 школ этого направления.
• На первом этапе ребенок учится считать при помощи абакуса. Это прибор, похожий на счёты.
• На следующем этапе дети откладывают настоящие абакусы в сторону и переходят на воображаемые. Теперь они только представляют этот прибор в уме и считают, мысленно передвигая косточки.
• Как раз в этот момент начинается самая большая польза от занятий. Почему? Сейчас объясним.

Положительный эффект от занятий ментальной арифметикой

Собственно зачем ребенку уметь делать такие сложные вычисления в уме? Ведь удобные калькуляторы есть в любом смартфоне.

Быстрые вычисления в уме – это не самоцель.

Когда дети переходят к работе с «мысленными абакусами», в работу включается воображение, концентрация внимания. То есть, задействуется правое полушарие головного мозга.

В это же время синхронно работает и развивается левое полушарие, отвечающее за логику и счет.

Таким образом мышление ребенка с детства «привыкает» решать жизненные задачи двумя полушариями головного мозга одновременно: сконцентрироваться на вопросе, вообразить какую-то схему и логически решить эту задачу. Очень быстро возникает креативный и в то же время логический подход к решению вопросов.

Итак

• Ребенок учится делать сложные вычисления в уме и удивлять окружающих. Растет его самооценка и уверенность в себе
• Развивается кратковременная, долговременная и фотографическая память, концентрация внимания, как следствие – повышается успеваемость в школе
• Ребенок с детства учится решать жизненные задачи, задействуя оба полушария головного мозга сразу: сконцентрировался, вообразил схему решения, быстро нашел креативное и логически обоснованное решение вопроса.

Преимущества нашего курса

• Все ученики получают доступ к порталу с упражнениями, чтобы ребенок мог тренироваться каждый день самостоятельно по 10 минут, а родитель мог отслеживать прогресс
• Каждый урок всего курса прописан по минутам. Ученики получают рабочие тетради, в которых к каждому занятию предусмотрено определенное количество упражнений. Преподаватель отпускает ребенка когда убедится, что все они выполнены корректно и ребенок усвоил материал.
• Стоимость пропущенных занятий не пропадает: мы «перебрасываем» эти деньги на депозит, который можно впоследствии использовать для посещения занятий и мастер-классов творческих направлений.

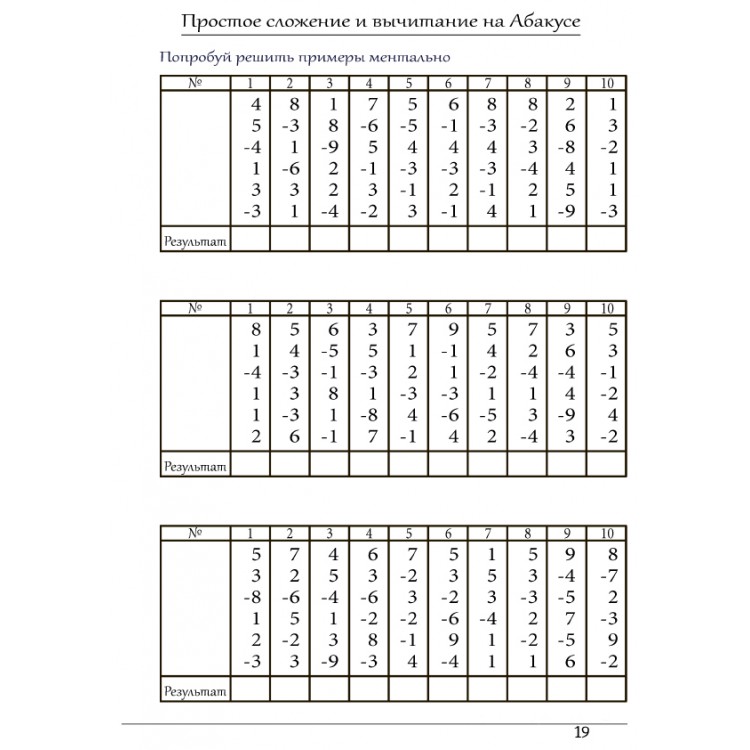
Результаты детей 5-6 лет:

Через 4 месяца занятий: Дети умеют складывать и вычитать на абакусе двузначные числа, а в уме они считают легкие примеры с двузначными числами и одинаковыми цифрами, например 11+66-55+77 и т.д.

Через 8 месяцев занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме они решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.

Через полтора года занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.

Через 3 года занятий (к 8 годам): Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.

Результаты детей 6-7 лет:

Через 2 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, а в уме считают легкие примеры с двузначными числами и одинаковыми цифрами, например 11+66-55+77 и т.

д.

Через 4 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме они решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.

Через 1 год занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.

Через 2,5 года занятий: Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.

Результаты детей старше 8 лет

Через 2 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.

Через 9 месяцев занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.

Через 2,5 года занятий: Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.

Организационные моменты

Расписание: занятия проводятся 1 раз в неделю по 2 академических часа.

Общая продолжительность курса: 2,5-3 года.

Запишитесь на пробное занятие по телефону +7 495 724 19 04 или заполнив форму на этом сайте.

Ментальная арифметика для детей. Развитие ребенка. Развитие памяти, логики, внимания. Развивающие занятия для детей

Подробная информация о курсе

Ментальная арифметика — это методика, по которой дети научатся быстро совершать в уме сложные арифметические вычисления (от скоростного сложения 100+ чисел до операций с десятичными числами и извлечения корней). 

Кому можно заниматься ментальной арифметикой? 

Ментальная арифметика показана всем детям от 4 лет, которые:

• Умеют считать от 1 до 10.
• Умеют соотносить изображение цифры с ее названием.
• Умеют писать цифры.
• Имеют развитую мелкую моторику.

Как работает ментальная арифметика? 

Счет на абакусе
Дети учатся считать на абакусе — древних китайских ментальных счетах.

Представление
Дети решают примеры, представляя абакус мысленно. Ребенок учится концентрироваться до тех пор, пока не решит пример.

Автоматизм
Действия доводятся до автоматизма и примеры усложняются. С увеличением сложности, количество объектов возрастает и развивается распределение внимания.

Формулы
Запоминание большого количества формул. У детей развивается краткосрочная память при решении примеров. Долгосрочная — при запоминании формул Фотографическая — при работе с флеш-картами.

Занятия по ментальной арифметике дают детям многое: 

Развивается мышление, творческий потенциал, воображение
Ваш ребенок начинает думать на несколько шагов вперед и применять знания для решения конкретных задач.

Развиваются навыки выполнения сложных расчетов в уме
Занятия по математике выходят на новый уровень

Повышается концентрация внимания ребенка

Ваш ребенок успешнее справляется с заданиями в школе и дома

Улучшается поведение, появляется уверенность в себе
Ваш ребенок сможет смело общаться со сверстниками и взрослыми, находить друзей

Программа полного курса включает в себя 6 уровней обучения:

Уровень S 
Знакомство с абакусом, его составляющими, правилами работы с ним

Длительность: 3 месяца

Результат: дети узнают как правильно складывать и вычитать на абакусе. Активно развивается навык мелкой моторики: почерк, манипуляция с мелкими предметами. Первые заметные улучшения успеваемости в школе.

Уровень M

Закрепление навыков, изучение формул счета

Длительность: 3 месяца

Результат: ребенок начинает считать по формулам. Ощутимо улучшается память и концентрация внимания. Заметно лучше запоминаются стихотворения, и виден прогресс в артикуляции.

Уровень А
Доведение техник сложения и вычитания до автоматизма

Длительность: 5-6 месяцев

Результат: дети могут посчитать любые примеры на сложение и вычитание за считанные секунды. Феноменально развиваются воображение, представление и фотографическая память.

Уровень R
Умножение на абакусе

Длительность: 3 месяца

Результат: молниеносный ментальный счет, доскональное знание и оперирование таблицей умножения, увеличение скорости счета. Значительно вырастает способность к аналитической деятельности, самостоятельность и заметно повышается самооценка.

Уровень T
Техника деления на абакусе

Длительность: 3 месяца

Результат: ребенок делит на абакусе, используя уже изученные формулы. На этом этапе ребенок тратит минимальное время на решение любых арифметических задач в школе. Многие дети занимают призовые места на олимпиадах.

Уровень Y
Техника счета отрицательных и десятичных чисел, квадратных и кубических корней на абакусе

Длительность: 3 месяца

Результат:  ребенок не только с легкостью подходит к решению любых задач как в школе, так и в жизни. Активно выражено стремление к лидерству, умение аргументированно отстаивать свою точку зрения, улучшается успеваемость по большей части предметов в школе.

Занятия на курсе по ментальной арифметике ведут сертифицированные преподаватели, в группах до 6 детей.
Для достижения результатов ребенку необходимо ежедневное выполнение домашних заданий (15 минут в день).

Дошкольники занимаются 2 раза в неделю, продолжительность каждого занятия — 60 минут. 
Школьники занимаются 1 раз в неделю, продолжительность занятия — 105 минут.  

Дополнительно приобретается комплект учебных материалов. 

Ваня у мамы силен в математике

Дошкольник Ваня Костромин из Ростова-на-Дону решает примеры быстрее старшеклассника. Юный вундеркинд занимается по специальной программе, в основе которой — обучение на счетах абакус, придуманных в Китае пять тысяч лет назад.

Юный ростовчанин увлекся ментальной арифметикой, инструментом которой и служат древние счеты, год назад. Сейчас он легко решает всего за четыре секунды десять примеров с двузначными цифрами на сложение и вычитание. Собственный рекорд Ивана — десять примеров за три секунды. Впереди у Ивана — умножение и деление, но таблицу умножения он уже знает и может умножить трехзначное число на однозначное.

— 391 умножить на 3, получится 1172, — демонстрирует детсадовец свои знания.

— Ванечка, на единичку ошибся, — поправляет его мама Анастасия.

— Да-а! — не огорчается малыш и тут же в считанные секунды одерживает собственную маленькую победу — решает 20 примеров на скорость две минуты девять секунд.

Цифры появляются на экране мобильного телефона Вани, куда закачана обучающая программа. Мальчик называет ответ, который совпадает с проверочным значением.

— На этот раз потребовалось больше времени, чем обычно, — объясняет Анастасия, — потому что Ваня выполнял два задания одновременно. Проще говоря, решал в уме два примера с различными действиями на сложение и вычитание.

На счетах пятилетний малыш уже умножает пятизначные цифры. Родные чуть ли не с самого его рождения уделяли много времени развитию мальчика. Сначала образованием ребенка занималась бабушка, преподаватель музыки, разучивала с малышом песни. Когда многие дети только начинают ходить, Ваня уже знал все буквы и цифры до десяти.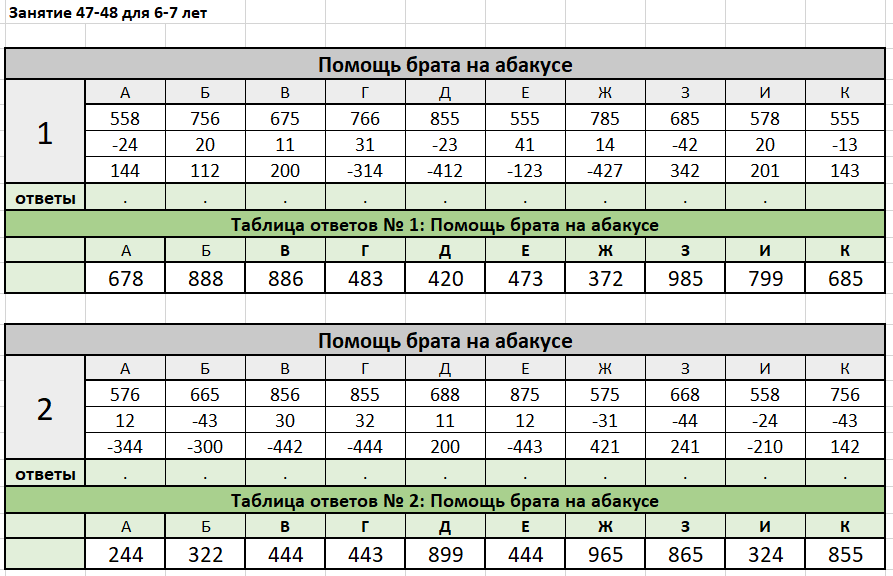 В три года родители купили сыну хороший мобильный телефон, чтобы ребенок решал на нем примеры самостоятельно. Играли с ним в различные логические игры.

Ваня самостоятельно прочитал уже восемь детских книг. Узнав о ментальной арифметике, Костромины сразу поняли: это то, что нужно их ребенку. Настя показала сыну счеты и рассказала, как ими пользоваться. Ване понравилось. Он стал заниматься дома и в детском развивающем центре.

Несмотря на то что у него «большой ум», как объясняет свои способности сам Иван, он ведет себя как самый обычный малыш его лет, очень подвижный и шустрый. Недавно мальчик стал финалистом международного детского конкурса по ментальной арифметике, на который приехали участники из 11 стран мира.

Таланты Вани не ограничиваются только успехами в математике. Методика, по которой он занимается, развивает сразу оба полушария мозга. Наверно, поэтому мальчик с легкостью запоминает любую информацию, впитывает знания как губка. Играет в шахматы, учит английский, а с недавних пор и японский. Любит петь песни и читать стихи, причем запоминает четверостишия с третьего прочтения.

Ответы на вопросы о нашем курсе ментальной арифметики

На какие разделы делится курс?

1. Уровень S
Длительность: 3 месяца
Программа: Знакомство с абакусом, его составляющие, правила работы с ним.
Результат: Дети узнают как правильно складывать и вычитать на абакусе. Активно развивается навык мелкой моторики: почерк, манипуляция с мелкими предметами. Первые заметные улучшения успеваемости в школе.

2. Уровень М
Длительность: 3 месяца
Программа: Закрепление навыков, изучение формул счета.
Результат: Ребенок начинает считать по формулам. Ощутимо улучшается память и концентрация внимания. Заметно лучше запоминаются стихотворения и виден прогресс в артикуляции речи.

3. Уровень А
Длительность: 5-6 месяцев
Программа: Доведение техник сложения и вычитания до автоматизма.
Результат: Дети могут посчитать любые примеры на сложение и вычитание за считанные секунды. Феноменально развиваются воображение, представление и фотографическая память.

4. Уровень R
Длительность: 5-6 месяцев
Программа: Подготовка к умножению на абакусе.
Результат: Молниеносный ментальный счет, доскональное знание и оперирование таблицей умножения, увеличение скорости счета. Значительно вырастает способность к аналитической деятельности, самостоятельность и заметно повышается самооценка.

5. Уровень T
Длительность: 5-6 месяцев
Программа: Умножение на абакусе.
Результат: Ребенок умножает на абакусе, используя уже изученные формулы. На этом этапе ребенок тратит минимальное время на решение любых арифметических задач в школе. Многие дети занимают призовые места на олимпиадах.

6. Уровень Y
Длительность: 5-6 месяцев
Программа: техника счета деления на абакусе.
Результат: Ребенок не только с легкостью подходит к решению любых задач как в школе, так и в жизни. Активно выражено стремление к лидерству, умение аргументировано отстаивать свою точку зрения, улучшается успеваемость по большей части предметов в школе.

 

Можно ли обучить своего ребенка самостоятельно?

Вы можете заниматься со своим ребенком индивидуально, пройдя обучение данной методике. Даже если вы решили заниматься сами, советуем проводить занятия в группе, поскольку групповые занятия развивают коммуникабельность, умение работать в команде.

 

Насколько эффективны эти занятия? Есть ли реальный прогресс?

Ментальная арифметика развивает творческое и аналитическое мышление, улучшает концентрацию внимания, фотографическую память, воображение, логику, а также наблюдательность и слух. Это не обычный счет в уме, ведь умение находить ответ на самые сложные примеры и задачи в считанные секунды развивает правое полушарие мозга, отвечающее за воображение и представление.

 

Не противоречит ли обучение ментальной арифметике школьной программе?

Обучение ментальной арифметике помогает ребенку лучше усваивать школьную программу. Во-первых, он развивает способности, связанные с памятью, воображением, логикой и мышлением. Во-вторых, помогает лучше понимать точные науки: математику, физику, геометрию. А в-третьих, придает уверенности детям. Когда ваш ребенок научится быстро считать и делать это лучше взрослого, он будет знать, что может научиться всему, нужно лишь постараться!

 

Ребенок может решать такие примеры на калькуляторе, зачем ему ментальная арифметика?

Абакус сложно сравнить с калькулятором, т.к. калькулятор вызывает леность ума, в то время как абакус заставляет мозг работать, что позволяет решать арифметические задачи со скоростью калькулятора. Кроме того, занятия ментальной арифметикой не только повышают скорость устного счета, но и развивают другие когнитивные способности ребенка (воображение, память, внимание, наблюдательность).

 

 

Ментальная арифметика — Яркий ум

Сейчас ментальная арифметика, как и любой необходимый и популярный продукт, попала под прицел различных плагиаторов, которые маскируясь под Центры ментальной арифметики стараются продать родителям детей некачественный образовательный продукт. Однако все это становится заметно уже через несколько месяцев уроков в такой школе. Дети, не усвоившие основу программы, не в состоянии двигаться дальше, а причина в том, что мозг не функционирует в связке, что является базой данного обучения.  

Есть ряд признаков, которые могут помочь вам выявить качественная это школа или же это просто самоучки, которые сами толком не разбираются в предмете:

— Настоящий Центр имеет все необходимые законные документы, дающие ей право обучать по данной методике.

— Есть материалы, в которых показаны все результаты обучения.

 

Сейчас ментальная арифметика, как и любой необходимый и популярный продукт, попала под прицел различных плагиаторов, которые маскируясь под Центры ментальной арифметики стараются продать родителям детей некачественный образовательный продукт. Однако все это становится заметно уже через несколько месяцев уроков в такой школе. Дети, не усвоившие основу программы, не в состоянии двигаться дальше, а причина в том, что мозг не функционирует в связке, что является базой данного обучения.  

Есть ряд признаков, которые могут помочь вам выявить качественная это школа или же это просто самоучки, которые сами толком не разбираются в предмете:

— Настоящий Центр имеет все необходимые законные документы, дающие ей право обучать по данной методике.

— Есть материалы, в которых показаны все результаты обучения.

— Имеются отзывы и замечания родителей дети, которых проходят обучение или уже закончили его.

— Каждый педагог прошел очную форму обучения и имеет именной сертификат на ведение преподавательской деятельности.

— У каждого родителя есть возможность дать своему ребёнку время на пробное обучение, чтобы он понял, подходит оно ему или нет.  

— Преподаватели могут дать рекомендацию родителям детей, чтобы они пришли спустя какое-то время, если будет заметно, что сейчас ребенок не испытывает особого желания учиться. Для Центра ментальной арифметики очень важно соблюдать стандарт качества своих услуг и показать успешный результат обучения.

— Качество работы обязательно проходит контроль со стороны материнской организации.

— Преподаватели всегда могут помочь решить те или иные вопросы в обучении ребенка.

— Вся методика и все программы постоянно видоизменяются и улучшаются, вносятся необходимые коррективы по ходу обучения.

— Учащиеся обеспечиваются всеми необходимыми материалами. Обучение ведется по специально разработанным учебникам и рабочим тетрадям.

— Весь базовый материал, история создания и развития Центра эксклюзивный. Он не списан с других ресурсов и все это можно очень быстро проверить.

Если выбранная вами школа ментальной арифметики удовлетворяет вышеперечисленным критериям, вы можете быть уверенны в том, что ребенок получит качественные знания и в ближайшее время вы увидите положительный результат обучения.

Сколько времени занимает обучение ментальной арифметике?

О ментальной арифметике на пространстве бывшего СНГ узнали совсем недавно. Однако все больше и больше родителей начинают интересоваться данной методикой и отдают своих детей в специализированные центры ментальной арифметики.

Вдохновленные роликами из Youtube, родители ждут, что буквально через месяц их чадо будет за доли секунды выдавать решение сложнейших примеров… И когда этого не происходит, многие разочаровываются, начинают думать, что их ребенок не способен стать гением, как те детки из роликов, бросают занятия….

Разбираться с тонкостями обучения ментальной арифметики, будем на примере центра «Яркий Ум». Разрабатывая данную методику мы изучили  Японскую, Корейскую, Малазийскую,

Индийскую и Китайскую школу МА. Здесь детям предлагают многоступенчатую систему обучения. На первом этапе происходит знакомство с абакусом, навыками сложения и вычитания с помощью него. По окончании уровня родители отмечают, что у детей повышается усидчивость, улучшается память и внимание. Как правило обучение длится около 3 месяцев. Однако, все зависит от возраста ребенка и его способностей. Некоторые усваивают программу за 2 месяца, а кому-то может потребоваться до полугода. Все очень индивидуально! Ведь кто-то имеет склонность к точным наукам и быстро сообразит что к чему, а кто-то выраженный гуманитарий, которому потребуется чуть больше времени.

Начиная со второй ступени обучения, дети складывают и вычитают однозначные числа уже в уме, без использования абакуса. На этом этапе хорошо развивается фотографическая память.

И только на третьей ступени дети начинают показывать удивительные результаты! Например, читать стихи и одновременно складывать в уме трехзначные числа!

Таким образом, примерно через 7-8 месяцев обучения родители смогут похвалиться, что их ребенок не только хорошо учится в школе и имеет хорошую память, но и умеет считать в уме быстрее калькулятора!

Ментальная арифметика не является чудом сама по себе. Она творит чудеса с мозгом ребенка, заставляя его развиваться и демонстрировать удивительные результаты. Для этого нужно время!

Дорогие родители, помните, что значительных успехов можно достичь только благодаря регулярным занятиям, соблюдению всех рекомендаций педагогов и главное, вере в способности вашего ребенка!

Реши примеры worksheet

Advanced search

Content:

Language: AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan Standard, Tibetan, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld Church Slavonic, Church Slavonic,Old BulgarianChuvashWelshDanishGermanDivehi, Dhivehi, MaldivianDzongkhaEweGreek (modern)EnglishEsperantoSpanishEstonianBasquePersian (Farsi)Fula, Fulah, Pulaar, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish Gaelic, GaelicGalicianGuaraníGujaratiManxHausaHebrew (modern)HindiHiri MotuCroatianHaitian, Haitian CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut, GreenlandicKhmerKannadaKoreanKanuriKashmiriKurdishKomiCornishKyrgyzLatinLuxembourgish, LetzeburgeschGandaLimburgish, Limburgan, LimburgerLingalaLaoLithuanianLuba-KatangaLatvianMalagasyMarshalleseMāoriMacedonianMalayalamMongolianMarathi (Marāṭhī)MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern Punjabi, Eastern PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (Saṁskṛta)SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Tonga Islands)TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu    Subject:   

Grade/level:    Age: 3456789101112131415161718+

Search: All worksheetsOnly my followed usersOnly my favourite worksheetsOnly my own worksheets

Ментальная арифметика

Раздел 1

Теория: Знакомство с детьми. Инструктаж по ТБ детей. Знакомство с ментальной арифметикой. Абакус и его конструкция: «братья» и «друзья». Правила передвижения бусинок, использование большого и указательного пальцев.

Раздел 2.

Теория: Знакомство с числами 1-4 на абакусе. Изучение цифр 1-4 на абакусе. Добавление и вычитание на абакусе чисел 1-4. Изучение чисел 5-9 на абакусе. Добавление и вычитание на абакусе чисел 5-9. Выполнение заданий на простое сложение и вычитание в пределах 1-9.

Раздел 3.

Теория: Набор чисел от 10 до 99. Определение чисел с абакуса. Выполнение упражнений на простое сложение и вычитание в пределах 10-99

Раздел 4.

Теория: Набор трехзначных чисел от 100 до 999 на абакусе. Определение чисел с абакуса в пределах 100-999. Простое сложение в пределах 100-999. Решение примеров на простое сложение в пределах 100-999. Простое вычитание в пределах 100-999. Решение примеров на простое вычитание в пределах 100-999. Выполнение упражнений на простое вычитание и сложение в пределах 100-999

Раздел 5.

Теория: Сложение с 5 методом «Помощь брата». Формулы добавления чисел 1-4. Базовые упражнения на сложение с 5. Решение примеров на сложение методом «Помощь брата«.

Вычитание с 5 методом «Помощь брата». Формулы вычитания чисел 1-4. Базовые упражнения на вычитание с 5. Выполнение примеров методом «Помощь брата». Сложение и вычитание с 5 методом «Помощь брата». Решение примеров на сложение и вычитание с 5 методом «Помощь брата» Раздел 6.

Теория: Сложение с 10 методом «Помощь друга». Формулы добавления чисел 1-9. Базовые упражнения на сложение с 10. Решение примеров на сложение с 10 методом «Помощь друга«.

Вычитание с 10 методом «Помощь друга». Формулы вычитания с 10 методом «Помощь друга». Базовые упражнения на вычитание с 10. Решение примеров на вычитание с 10 методом «Помощь друга». Выполнение заданий на сложение и вычитание с 10 методом «Помощь друга»

Раздел 7.

Теория: Сложение комбинированным методом. Формулы и базовые упражнения сложения комбинированным методом.

Вычитание комбинированным методом. Формулы и базовые упражнения вычитания комбинированным методом

Раздел 8.

Теория: Многозначные числа. Простое сложение вычитание многозначных чисел.

Сложение и вычитание многозначных чисел с 5 и с 10, методами «Помощь брата», «Помощь друга», комбинированным методом.

Abacus — Cuemath

Знаете ли вы, что Cranmer Abacus специально разработан для работы слепых людей?

Счеты помогают нам понять математические концепции, развивая чувство числа, чего не всегда можно достичь с помощью калькулятора.

В этом мини-уроке мы узнаем о счетах — как использовать, калькуляторе и изучении счеты, поскольку мы изучим понятие счеты.

План урока

Что такое счеты?

Счеты — это простое счетное устройство, состоящее из бусинок, размещенных в стержнях проволоки, заключенных в деревянную раму.

Расчеты можно производить, сдвигая валики по стержням.

Части Abacus

Различные части абака:

• Внешняя граница счет называется рамкой.
• Счеты, которые мы используем в настоящее время, имеют 17 стержней, и на каждом стержне 5 бусинок.
• В счетах два деления. Горизонтальная планка, разделяющая верхнюю и нижнюю часть, называется балкой.
• Бусинки, находящиеся в нижней части, называются нижними бусинками или земляными бусинками.
• Бусинки, находящиеся в верхней части, называются верхними бусинами или небесными бусинками.

---

Как считать числа на счетах?

Счеты — это устройство, которое можно использовать для счета, сложения, вычитания, умножения и т. Д.

• Крайний правый столбец — для своего места.
• Следующий столбец используется для разряда десятков.
• Третий столбец справа предназначен для разряда сотен и так далее.{\ text {rd}} \) в правом нижнем углу.

2. Считаем 8 в верхнем и нижнем ряду:

• Используйте 1 бисеринку из верхнего ряда, что эквивалентно 5 и 3 бисеринкам из нижнего ряда.
• Таким образом, расчет даст ответ 5 + 3 = 8.

В следующей таблице показаны различные счетные устройства, подобные счетам, используемые в разных странах:

Страна	Устройство
Китай	Суанпан
Япония	Соробан
Россия	Чоты

---

Как сложить и вычесть с помощью Abacus?

Как только вы научитесь использовать счет для счета, вы сможете использовать его для множества других операций.

Дополнение

Стратегия 10

Если нам нужно сложить 8 + 6, мы введем 6 и 8 в первые два столбца.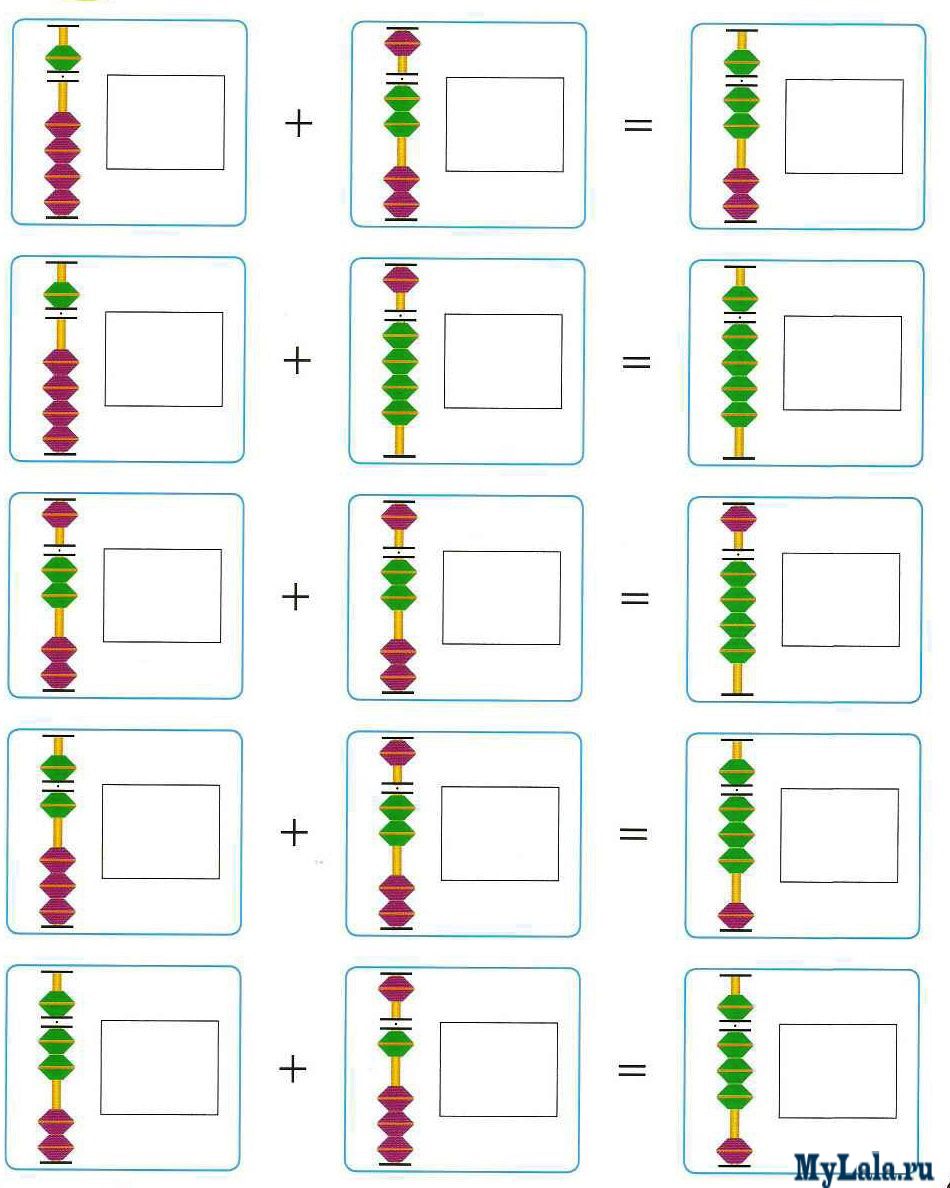

Затем перейдите от 6 к 8 так, чтобы 8 стало 10, а 6 стало 4.

Итак, теперь мы можем легко использовать 10 + 4 = 14.

Освоив эту стратегию на счетах, вы можете попробовать сделать это мысленно.

Стратегия двух пятерок

Если нам нужно сложить 6 + 8, мы введем 6 и 8 в первые два провода.Две пятерки сделают 10, а у нас останется 4 бусинки. Теперь выполнить 10 + 4 = 14 легко.

Эта стратегия работает в задачах, где два добавляемых числа больше пяти.

Добавление больших чисел

Предположим, мы должны сложить 57 + 86. Нам нужно будет представить 86 на счетах.

У первого провода справа будет 6, а у второго — 8. Начните с первого провода и прибавьте 7 к 6. В результате получится 13.

Сохраните цифру 3 и перейдите от 1 к 8, получив таким образом 9.

Теперь выполните 9 + 5, в результате получится 14.

Итак, фактический результат будет 143.

Вычитание

Процесс вычитания противоположен сложению.

Нам просто нужно заимствовать цифры из предыдущего столбца, а не переносить их.

Пример

Если мы хотим вычесть 672 из 945,

• Введите 945 на счетах и ​​начните вычитать столбец за столбцом слева.
• I Если мы вычтем 2 из 5, то получим 3 вместо единицы.
• Используйте аналогичный метод для десятичных разрядов. Поскольку мы не можем вычесть 7 из 4, нам придется занять 1 из разряда сотен, оставив 8 в разряде сотни. Теперь мы получим 14 в десятке. Вычитая 7 из 14, получаем 7 в разряде десятков.
• Наконец, вместо сотни мы вычтем 6 из 9, и таким образом у нас останется 3 бусины.

Итак, наш окончательный ответ будет 945 — 672 = 273.

Калькулятор абак

Попробуем решить математические операции с помощью следующего калькулятора абак:

---

Каковы преимущества использования Abacus?

На счетах:

• Улучшает умственные арифметические вычисления
• Повышает концентрацию
• Обостряет память
• Улучшает воображение
• Повышает уверенность
• Повышает навыки решения проблем

1. Abacus — это полезное обучающее оборудование для слабовидящих, а также для всех, кто хочет изучить происхождение современного калькулятора.
2. Бусинки в верхнем стержне, имеющие значение 5, называются го-дама, а 4 бусинки в нижнем ряду, каждая из которых имеет значение 1, известны как ичи-дама.

Решенные примеры

Можете ли вы помочь Марте изобразить число 3687 на счетах?

Решение

Число 3687 можно представить на счетах следующим образом:

• Сдвиньте 2 бисеринки вверх в нижнем ряду и 1 бисеринку вниз в верхнем ряду в крайнем правом столбце.{\ text {th}} \) столбец справа.

Лиззи застряла в проблеме при сложении двух чисел. Можете ли вы помочь ей, записав шаги, чтобы сложить 456 и 796, используя счеты?

Решение

Шаги для вычисления суммы 456 и 796:

• Нам нужно будет представить 796 на счетах.
• Первый провод справа будет иметь 6, второй провод 9 и третий провод 7.
• Начните с первого провода и прибавьте 6 к 6. В результате получится 12. Сохраните цифру 2 и перейдите от 1 к 9, таким образом получится 10.
• Теперь выполните 10 + 5, что даст 15. Оставьте 5 и перенесите 1 на следующий провод.
• Теперь сложите 8 (7 + 1) и 4, и в результате получится 12.

Итак, результат будет 1252.

\ (\ следовательно \) Sum = 1252

Майк учится представлять числа на счетах.Можете ли вы сказать ему, какое число представлено на следующих счетах:

Решение

Бусины на счетах имеют следующий вид:

• 4 на месте
• 2 в десятке
• 1 в сотках
• 3 на сотках

Итак, представленное число = 3124.

\ (\ следовательно \) Представленное число = 3124

Какие операции можно выполнять на счетах?

Решение

На счетах можно выполнять следующие операции:

• Дополнение
• Вычитание
• Дивизион
• Умножение

• Как бы вы использовали счеты для умножения и деления?

Интерактивные вопросы

Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

---

Подведем итоги

Мини-урок был посвящен увлекательной концепции счётов. Математическое путешествие по счетам начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано так, чтобы не только было понятно и легко понять, но и навсегда осталось с ними.В этом заключается магия Куэмат.

О компании Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.

---

Часто задаваемые вопросы (FAQ)

1. Что такое полная форма счеты?

Полная форма абака — это система «Изобилие бусинок, сложения и вычислений».

Это простое счетное устройство, состоящее из бусинок, размещенных в стержнях проволоки, заключенных в деревянную раму.

2. Чем полезны счеты в математике?

Abacus — это устройство, которое можно использовать для выполнения математических операций, таких как сложение, вычитание, умножение и деление.

Таким образом, это помогает сократить время при выполнении математических вычислений с большей эффективностью.

3. Как вы представляете числа на счетах?

Счеты — это устройство, которое можно использовать для счета, сложения, вычитания, умножения и т. Д.

Числа могут быть представлены как:

• Крайний правый столбец — для своего места.
• Следующий столбец используется для разряда десятков.
• Третий столбец справа предназначен для разряда соток и так далее.

abacus math

Covid-19 привел мир к феноменальному переходу.

Электронное обучение — это будущее сегодня.

Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!

Abacus math — это инструмент, состоящий из палочек и бусинок. Палки представляют собой место числа, а бусинки используются для чисел. 1-я палка справа — это единиц или единиц, а вторая палка — единиц. Для 1-го класса математики мы будем обсуждать только двузначное число.

Как писать цифры на счетах

На картинке выше есть две палочки. Один с правой стороны — это палка с разметкой одного места или единицы, а следующая — палка с десятками.
Теперь есть,
две бусинки в десятке = 20
Бусинок на месте нет = 0
Таким образом, получается число 20.

На картинке выше
1 бусина в десятке = 10
3 бусинки one place stick = 3
Итак, число 13.
Таким образом, мы можем записывать числа, используя счеты.

Написание числовых имен

Числа Четыре

Семнадцать 9

Числа	Числовые имена	Числовые имена	Числовые имена	Числа		Один	11	Одиннадцать	30	Тридцать
2	Два	9	12 40	Сорок
3	Три	13	Тринадцать	50	Fifty 417	Fifty 417	1 4	Четырнадцать	60	Шестьдесят
5	Пять	15	70 Fifteen
6	Шесть	16	Шестнадцать	80	Восемь
7		90	Девяносто
8	Восемь	18	Восемнадцать	10017	10017	Девять 9 0017	19	Девятнадцать
10	Десять	20	Двадцать

У ребенка есть только написание этих имен и остальные имена номеров, которые он / она может написать, используя указанные выше имена номеров.
Пример 1: 35
В 35, 3 в разряде десятков = 30 (Тридцать)
И 5 в разряде единиц = 5 Пять
Соедините эти имена чисел вместе, так что
35 = Тридцать пять

Пример 2: 48
В 48, 4 в разряде десятков = 40 (Сорок)
И 8 в разряде единиц = 8 Восемь
Соедините эти имена чисел вместе, так что
48 = Сорок восемь

---

Abacus Math

1st Grade Math

Home

Covid-19 повлиял на физическое взаимодействие между людьми.

Не позволяйте этому влиять на ваше обучение.

Некоторые примеры чисел на счетах. (Адаптировано из Heffelfinger …

Context 1

… Тест базовых фактов сложения был использован для оценки базовых знаний детей о фактах сложения и используемых ими стратегий. Тест содержал 40 дополнительных задач, сгруппированных в 6 категорий следующим образом : Сложение 1, 2 и 3, добавление 0, перекрытие 10, почти двойные, двойные и десятки фактов.От детей требовалось дать ответ устно и объяснить стратегию, которую они использовали, чтобы прийти к ответу по каждому пункту. Каждый ребенок был проверен на тесте основных фактов сложения. Для прохождения теста всех детей по отдельности отвели в отдельную комнату, которая была пристроена к их классу. Задачи на сложение задавались по одной на карточках, и детям предлагалось использовать любую стратегию, которая позволяла им быстрее найти ответ. Их поощряли высказывать свои мысли вслух, и им велели продолжать говорить столько, сколько они могли.Стратегии были классифицированы как подсчет всего по сумме, расчет от первого слагаемого, расчет от большего слагаемого, мин, счеты, отзыв, визуализация счётов и угадывание. Шаг 2 — Наблюдение в классе. Наблюдения проводились в течение двух недель для каждого уровня детского сада по мере того, как учитель внедрял запланированную учебную программу для добавления. Исследователь и один обученный наблюдатель наблюдали за каждым классом. Во время этих наблюдений взаимодействие учителя и детей записывалось на видео, и делались записи, в которых описывалось, чем занимались дети, и общие впечатления от класса.Исследователь просматривал и просматривал записи учителей, добавляя информацию из полевых заметок, пока не были собраны достаточно полные записи. Счеты были впервые представлены, когда дети были в K1; Дети K2 начали приобретать больший опыт работы со счетами, а детям открыто давали инструкции и давали много упражнений по использованию счеты. Казалось, что большинство детей очень хорошо владеют счетами в K3. Результатом обучения математике для детей K1 является развитие однозначного соответствия и числовых комбинаций до 5.Детей также познакомили со счетами в K1. Ожидалось, что они научатся изображать числа от 1 до 5 на счетах, расположив бусинки в соответствующей форме. Результатом по математике для детей К2 является освоение комбинаций до 10. Проведены дополнительные уроки по счетам. Дети выучили правила использования счеты для простого сложения (см. Рис. 1 и 2). Когда на колонке недостаточно бусинок для завершения сложения или вычитания, используется методика использования комбинаций (дополнительных чисел) 5 и 10 (Heffelfinger & Flom, 2004).Следовательно, дети должны хорошо владеть комбинациями 5 и 10. Выполняя сложение, всегда вычитаются дополнительные числа. Две группы дополнительных чисел (4 и 1 и 3 и 2) используются для числа 5. Пять групп дополнительных чисел предназначены для числа 10 (9 и 1, 8 и 2, 7 и 3, 6 и 4 и 5 и 5. ). Например, в случае 4 + 8 нужно сначала подтолкнуть 4 бусинки на столбике B. Поскольку в столбце B недостаточно бусинок, чтобы представить 8, используется дополнительное число.Два — это дополнительное число 8 в составе 10. Затем прибавьте 8, вычитая дополнительное число 2, и перенесите единицу в столбец A (см. Рисунок 3). В K3 дети были хорошо знакомы со счетами. Они даже научились вычислять сложение и вычитание с помощью трех цифр. Было дано много упражнений на счетах. На наблюдаемых уроках детям обычно предлагалось решить группу похожих задач, пока они не овладели ими. В случае обучения 4 + 8 дети будут задавать аналогичные задачи, такие как 4 + 7, 3 + 8, 2 + 8, 9 + 7 и т. Д., Чтобы практиковаться, пока они не овладеют ими.Идея использования счётов заключалась в том, чтобы в конечном итоге помочь детям превратить механическое сложение и вычитание бусинок в визуализированные счеты в их сознании. На этапе K3 детей постоянно поощряли визуализировать в уме счеты при выполнении вычислений. Было обнаружено, что дети физически используют счеты только тогда, когда числа были больше и не могли найти ответ автоматически. Учитель активно отговаривал считать пальцами. На уровне K1, где детям было от 3 до 4 лет и в первый год их обучения в детском саду, только несколько детей пытались вычислить все дополнительные задания в тесте.В целом общий успех теста составил 20%. Большинство детей K1 использовали стратегию угадывания или не делали никаких попыток. Это открытие перекликается со стратегией уровня 1 в исследовании Гриффина (2003) с детьми детского сада. Гриффин обнаружил, что большинство детей в выборке в возрасте от 3 до 4 лет, ответили пустым выражением лица или сказали, что не знают ответа, вместо того, чтобы предпринять какие-либо попытки решить задачу 4 + 3. Тем не менее, результаты этого исследования также показывают, что дети K1 использовали ряд стратегий, включая сумму, минимум, стратегии угадывания для решения основных фактов сложения.Были свидетельства отзыва и визуализации счётов. В этом исследовании многие дети K1 легко запомнили 1 + 1 (86%), а некоторые вспомнили 2 + 2 (32%), но не другие факты. Эти дети K1 полагались на стратегии Sum, даже иногда они не могли прийти к правильным ответам. Был обнаружен только один ребенок, визуализирующий счеты. В возрасте от 4 до 5 лет дети в K2 были на втором году обучения в детском саду. Как и дети K1, результаты теста основных фактов показывают, что дети K2 испытывают трудности при вычислении основных фактов сложения, где слагаемые больше 5.Тем не менее, в целом они могли бегло вычислять (вспоминать) факты с добавлением меньше пяти. Среднее значение правильных ответов для проверки основных фактов составило 79,6%. В этом исследовании дети K2 использовали девять различных стратегий сложения: припоминание, производный факт, представленные или визуализированные добавления и напоминание факта, подсчет, минимум, сумма по материалам, сумма пальцами, угадывание и визуализация счётов. Однако чаще всего дети использовали суммированную стратегию с помощью пальцев или материалов.Это подтверждает предыдущие результаты исследований о том, что дети не всегда используют самые эффективные стратегии (Карпентер и Мозер, 1984; Кристенсен и Купер, 1991; Хулихан и Гинзбург, 1981). Хотя дети K2 использовали ряд стратегий, большинство из них автоматизировали многие факты (то есть использовали стратегию вспоминания), и у этих очень маленьких детей было 79,6% мастерства. Другой выявленной стратегией развития была стратегия визуализации счётов, которую использовали гораздо больше детей с K2, чем детей с K1.Было обнаружено, что в возрасте от 5 до 6 лет дети в группе K3 использовали шесть стратегий для добавления фактов: вспоминание, извлеченные факты, представленные или визуализированные дополнения и напоминание фактов, визуализированные счеты, минус (счет в уме) и счеты. Дети в K3 имели высокий уровень усвоения основных фактов, со средним групповым значением 99% по тесту основных фактов. Стратегия отзыва (48%) оказалась доминирующей стратегией, используемой детьми K3, а второй доминирующей стратегией были визуализированные счеты (31%). Дети часто использовали визуализированные счеты или стратегию счётов, когда они вычисляли факты, особенно с более крупными слагаемыми (например.g., Bridging 10, Near Doubles или Doubles). В тесте основных фактов есть шесть категорий дополнительных фактов. Это (1) сложение 1, 2, 3 фактов, (2) добавление 0 фактов, (3) соединение 10 фактов, (4) почти двойные факты, (5) удвоение фактов и (6) десятки фактов. В этом исследовании дети K1 потратили меньше всего времени на факты о двойниках и …

Расчетные инструменты и вспомогательные средства — Abacus

Счеты

Счеты, в частности счеты Кранмера, безусловно, являются одним из самых эффективных инструментов расчета для слепых детей, как для людей с низким, так и для отличных результатов, когда они используются отдельно или в сочетании с другими устройствами.Он позволяет выполнять конкретные манипуляции, приводя к более значимому пониманию чисел, чем использование калькуляторов, и предоставляет альтернативу длительным и сложным вычислениям, выполняемым на устройстве для записи шрифтов Брайля, хотя способность работать с этими двумя инструментами также очень важна и требует обсуждается в других местах в разделах «Шрифт Брайля как инструмент расчета» и «Говорящие калькуляторы». Фактически, совместное использование брайлевера и счётов может быть очень эффективным; учащиеся могут использовать счеты, чтобы проверить свою работу на шрифте Брайля, и, если есть несоответствие, переработать задачу, используя оба инструмента.Обычно рекомендуется, чтобы учащийся переходил от использования более громоздкого инструмента к менее громоздкому. Для некоторых студентов представление решения задач на счетах даже увеличило их способность к мысленным вычислениям.

Счеты также полезны из-за их скорости, точности, портативности и гибкости. Его можно использовать в образовательных целях, чтобы поддержать хорошую основу для сложения, вычитания, умножения и деления. Его также можно использовать для выполнения вычислений с использованием дробей и десятичных знаков, а также для помощи в выполнении арифметических операций, включенных в математику более высокого уровня.Его также можно использовать для навыков самостоятельной жизни, таких как запись телефонных номеров или подсчет затрат во время покупок.

Развитие навыков использования счётов

Умение пользоваться счетами зависит от нескольких факторов. Одно из них — готовность. Например, чтобы начать работать со счетами, дети должны понимать основные понятия чисел, уметь считать и знать партнеров или дополнения, составляющие числа до десяти. Эти концепции следует преподавать конкретно с помощью манипуляторов, формируя и переставляя наборы объектов.Студенты также должны узнать, что некоторые бусинки на счетах обозначают одну, другие пять, некоторые десять и т. Д., А также знать основную концепцию числовой стоимости. Работая с наборами, учащиеся могут ставить соответствующие числа на счетах. Узнав о числовой стоимости, они могут подкрепить эту концепцию счетами. По мере того, как они привыкают ко всем партнерам чисел до десяти, они могут устанавливать простые числовые выражения на счетах. Знакомство со счетами нужно начинать рано. Молодых студентов следует поощрять использовать его ограниченным образом при разработке числовых концепций; они могут использовать его как инструмент расчета позже, по мере развития своих навыков.

Студентам также необходимы манипулятивные навыки, необходимые для работы с самими счетами. Некоторые учителя предпочитают начинать детей с увеличенных счётов из-за более крупных бусинок и большего пространства между бусинами; затем студенты могут при необходимости перейти к меньшим счетам.

Третье требование для успеха ученика в работе со счетами — это компетентность и отношение его учителя. Учителя должны взять на себя ответственность за развитие своих навыков до уровня, достаточного для того, чтобы научить своих учеников навыкам, которые принесут им пользу.Учителя также должны выражать положительное отношение к использованию счётов, тому, как их использование — и усилиям, необходимым для того, чтобы научиться их использовать, — были полезными для ученика.

Подходы к обучению

Есть несколько подходов к обучению работе со счетами. Поскольку один метод может не работать эффективно для всех учащихся, учителя должны быть знакомы с несколькими методами. Наиболее часто используемые подходы:

• партнеры или логический подход,
• секреты подхода,
• метод подсчета, а
• адаптации или комбинации этих подходов.

Каждый из них кратко описан ниже с примером (3 + 4 = 7), разработанным в соответствии с этим подходом.

Логический метод или партнерский метод фокусируется на понимании «что» и «почему» шагов в решении проблемы на счетах. Это требует, чтобы учащийся знал партнеров или комплименты чисел до десяти (5 = 2 + 3, 5 = 1 + 4). Вербализация шагов и причин каждого движения на счетах — важная особенность этого подхода. Сначала учитель должен объяснить шаги и причины, по которым ученик работает над проблемой.Затем ученик должен озвучить процесс по мере того, как он или она работает над проблемой. Со временем этот «разговор» можно сократить, и, наконец, процесс станет внутренним. Такой подход принесет пользу студентам, которые могут следовать объяснениям и могут понимать задействованные логические концепции и даже получать от них удовольствие.

Пример: «Задача 3 + 4. Какое число стоит первым? Ответ — 3. Итак, мы ставим 3 на счетах. Теперь нам нужно добавить 4. Нам нужно добавить еще 4? Нет. Так как у нас недостаточно бусинок, мы можем добавить 5 бусинок (набор 5).Но 5 — это слишком много; мы хотели добавить только 4. Так что нам нужно убрать лишнюю бусину или бусинки. Что такое партнер 4 из 5? Ответ: 1. Итак, уберем одну лишнюю бусину. Каков наш ответ? Ответ — 7. »

Пример: «Задача 3 + 4. Какое число стоит первым? Ответ — 3. Установите 3. Можете ли вы установить 4 напрямую? Нет. Какое наименьшее значение, которое можно установить, больше 4? Ответ 5. Установите 5 бусинок. На сколько больше 5, чем 4? Ответ: 1. Очистите 1 бусинку. Какой ответ? Ответ 7.”

Метод секретов фокусируется на процессе перемещения бусинок на счетах в определенной последовательности, следуя определенному набору правил для различных чисел и операций. Это не подчеркивает понимание этого процесса, а скорее механическую память движений бусинок. Это было бы уместно для студентов, которые извлекли бы выгоду из манипулятивного процесса, на который они могли бы положиться, без полного понимания принципов, лежащих в основе каждого шага этого процесса.

Пример: «Задача 3 + 4.Какое число стоит первым? Ответ — 3. Итак, установите 3 (поднимите три фишки земли). Теперь мы хотим добавить 4. Для этого мы должны установить 5 (сбросить счетчик небес) и очистить 1 (сбросить один счетчик земли). Каков наш ответ? Ответ — 7. »

В методе подсчета учащийся считает каждую бусину по мере ее добавления или вычитания, переходя от единичных бусинок к 5 бусинкам (но считая только 1 для всех бусинок). Существуют также особые правила относительно определенных чисел и операций, но меньше, чем полный набор секретов.Это не подчеркивает понимание концепций, лежащих в основе движений бусинок. Этот подход также может быть подходящим для молодых людей, которые извлекли бы выгоду из манипулятивного процесса, на который они могли бы положиться, без необходимости понимать каждый отдельный шаг.

Пример: «Задача 3 + 4. Какое число стоит первым? Ответ — 3. Итак, мы устанавливаем 3. Теперь мы хотим добавить 4. Для этого мы поднимаем еще одну единичную бусинку (счет 1), затем еще одну единичную бусинку (счет 2), затем опускаем бусинку над счетной полосой. (сосчитайте 3) и уберите все четыре бусинки под счетной полосой.Наконец, поднимите еще одну бусину (сосчитайте 4). Какой ответ? Ответ — 7. »

Есть несколько доступных ресурсов, которые демонстрируют, как научить пользоваться счетами, используя вышеупомянутые подходы. Abacus Made Easy (Davidow, 1975) использует логический подход. Японские счеты: их использование и теория (Кодзима, 1954) описывает секретный подход. Abacus Basic Competency (Millaway, 1994) использует метод подсчета. Использование Cranmer Abacus (Ливингстон, 1997) объясняет как логический, так и счетный подходы.

Учителя слепых детей внесли множество изменений во все эти подходы, чтобы соответствовать индивидуальным стилям обучения своих учеников. Например, учащиеся, которые большую часть времени находятся в обычном классе, могут решать свои задачи на сложение и вычитание справа налево, чтобы они совпадали с тем, как учитель решает задачу с классом.

Пример более конкретной модификации относится к делению и иногда упоминается как «метод вычитания» деления.Делитель помещается в крайнее левое положение на счетах, затем остаются пустыми 2 столбца, за которыми следует делимое. Частное — это сумма частичных ответов, полученных учащимся по мере того, как учащийся работает над проблемой, и помещается в крайнее правое положение.

Другой конкретный пример модификации логического метода включает в себя умножение одно-, двух- или трехзначных множителей и одно- или двухзначных множителей. Например, в задаче 93×25 первый множитель (93) установлен в разрядах миллиардов, второй множитель (25) — в разрядах миллионов, а ответ — в разрядах тысяч и сотен.Вместо того, чтобы работать извне внутрь, все множимое умножается на первую цифру множителя; затем все множимое умножается на вторую цифру множителя.

Стратегии обучения работе со счетами

Помимо изменения общих подходов к обучению счетам, учителя нашли несколько стратегий, которые могут помочь облегчить обучение учащихся этому навыку. Некоторые из них включены здесь:

• Знакомство со счетами нужно начинать в раннем возрасте, когда ребенок начинает работать над числовыми понятиями; в начальных классах его можно использовать для поддержки изучения и понимания операций и вычислений, а также использования дробей и десятичных знаков.Его можно легко использовать вместе с пишущим шрифтом Брайля; К средней школе учащиеся должны уметь пользоваться счетами, что сокращает потребность в написании шрифтом Брайля. Рекомендации по сочетанию использования этих двух инструментов представлены в разделе «Инструменты и вспомогательные средства для расчетов».
• Важно, чтобы учащийся положительно относился к своим счетам. Одна учительница сказала своему ученику, что он выиграл его, что заставило его почувствовать себя особенным и захотеть его использовать. Предоставление простых, но актуальных заданий, в которых учащийся использует счеты, также будет полезно для мотивации учащегося.
• Счеты можно использовать для различных функциональных и мотивирующих занятий в классе, таких как подсчет очков в играх, подсчет баллов в ежедневных викторинах, использование в простых играх на деньги (1 = пенни, 5 = 5 центов, 10 = 10 центов).
• Такие игры, как «пчела» счётов, могут сделать изучение счётов ещё более увлекательным. Команды можно выбирать разными способами. Люди могут соревноваться с людьми в заранее определенном порядке, который может меняться. Очки или команды-победители могут быть определены разными способами.У каждого ученика должны быть свои счеты в этой или подобных играх.

Поскольку слепые ученики не могут видеть гештальт того, где их бусинки размещены на счетах, чрезвычайно важно научить их привычкам удерживать место. Это будет особенно важно, когда они имеют дело с задачами, включающими умножение, деление, десятичные дроби, дроби, а также любые задачи, связанные с нулями.

Две абачи, помещенные одна над другой или бок о бок, соединенные соединителем, можно эффективно использовать для записи и суммирования частичных произведений или ответов по одному при проработке дополнительных этапов задачи по другому.

Таблица секретов

Некоторое сложение и вычитание можно выполнять непосредственно на счетах Кранмера, то есть соответствующие бусинки можно перемещать без необходимости замены. Например, 3 + 1, или 5 + 2, или 8-5 могут быть выполнены напрямую, потому что перемещения бусинок с реальным значением достаточно для решения проблемы. Тем не менее, это не всегда так. В такой задаче, как 3 + 2, можно установить 3 бусинки, но еще 2 бусинки нельзя установить напрямую. Вместо этого необходимо установить пять бусинок и очистить четыре ранее установленных бусины.Логический метод заставит ученика вербализовать этот процесс. Секретный метод предлагает шаги по перемещению бусинок определенным образом, чтобы прийти к правильному ответу. Список этих секретов сложения и вычитания представлен ниже.

Число, которое нужно добавить, а затем секрет этого числа:

1. Набор 5, прозрачный 4
1. Прозрачный 9, набор 1 слева
2. Набор 5, прозрачный 3
2. Прозрачный 8, набор 1 слева
3. Набор 5, прозрачный 2
3. Очистить 7, установить 1 слева
4. Набор 5, прозрачный 1
4. Прозрачный 6, набор 1 слева
5. Прозрачный 5, набор 1 слева
6. Набор 1, прозрачный 5, набор 1 слева
6. Прозрачный 4, набор 1 слева
7. Набор 2, прозрачный 5, набор 1 слева
7. Прозрачный3, набор 1 слева
8. Набор 3, прозрачный 5, набор 1 слева
8. Прозрачный 2, набор 1 слева
9. Набор 4, прозрачный 5, набор 1 слева
9. Очистить 1, установить 1 слева

Число для вычитания, за которым следует секрет этого числа:

.

1. Очистить 1 слева, установить 9
1. Набор 4, прозрачный 5
2. Очистить 1 слева, установить 8
2. Набор 3, прозрачный 5
3. Очистить 1 слева, установить 7
3. Набор 2, прозрачный 5
4. Очистить 1 слева, установить 6
4. Набор 1, прозрачный 5
5. Очистить 1 слева, установить 5
6. Очистить 1 слева, установить 4
6. Очистить 1 слева, установить 5, очистить 1
7. Очистить 1 слева, установить 3
7. Очистить 1 слева, установить 5, очистить 2
8. Очистить 1 слева, установить 2
8. Очистить 1 слева, установить 5.прозрачный 3
9. Очистить 1 слева, установить 1
9. Очистить 1 слева, установить 5, очистить 4

Список литературы

Давидов, М. Э. (1977). Легкие счеты . Луисвилл, Кентукки: Американская типография для слепых.

Кодзима, Т. (1954). Японские счеты: использование и теория . Ратленд, Вермонт: Charles E. Tuttle Company, Inc.,

Ливингстон, Р. (1997). Использование счеты Cranmer, 2-е издание .Доступно на следующем сайте: www.tsbvi.edu/publications/abacus.htm

Миллавей, С. М. (1994). Базовая компетенция Abacus . Норристаун, Пенсильвания: полезные материалы для инвалидов по зрению.

Как пользоваться счетами — видео и стенограмма урока

Использование счеты

Чтобы прочитать счеты, вы посмотрите, какие бусинки куда перемещаются. Каждый столбец представляет собой разное разрядное значение. Крайний правый столбец представляет значение разряда отдельных единиц.Столбец рядом с ним представляет собой разряды десятков. Средний столбец представляет собой значение сотен разрядов.

Бусинки внизу — это числа от 1 до 5, а бусинки наверху — это 5 и 10 соответственно. Вы перемещаете верхние бусинки вниз и нижние бусинки вверх, чтобы обозначить число. Если вы сдвинете одну нижнюю бусинку вверх в столбце десятков, у вас будет номер 10. Если вы вытолкните две нижние бусинки из столбца сотен, у вас будет 200. Если вы сдвинете одну верхнюю бусину вниз из столбца десятков, вы получите есть 50.Чтобы представить число 15, вы должны нажать две верхние бусинки в крайнем правом столбце вниз и подтолкнуть пять нижних бусинок вверх. Вы также можете использовать два столбца, чтобы получить номер 15. Вы можете подтолкнуть одну нижнюю бусину вверх из второго столбца справа и пять нижних бусинок вверх в крайнем правом столбце.

Расчет с помощью бус

Теперь давайте посмотрим, как можно использовать счеты для решения своих математических задач.

Допустим, вы хотите вычислить 11 + 45. Вы бы начали с нажатия бусинок, чтобы получилось 11.Вы выталкиваете одну нижнюю бусину вверх из столбца десятков и одну нижнюю бусину вверх из столбца единиц.

Теперь, чтобы добавить 45, все, что вам нужно сделать, это добавить такое количество бусинок на свои счеты. Вы переместите четыре нижних бусинки вверх из столбца десятков и одну верхнюю бусину вниз в столбце единиц. Вы переместите одну верхнюю бусину вниз, так как каждая из этих верхних бусинок представляет собой 5 бусинок. Кроме того, не хватает нижних бусинок, чтобы подняться в столбце единиц.

Тогда ваш ответ — это число, указанное на ваших счетах. Чтение счеты дает 56 (50 из столбца десятков и 5 + 1 = 6 из столбца единиц).При достаточной практике вы сможете быстро и легко производить расчеты на своих счетах.

Другие примеры

Давайте теперь попробуем задачу на вычитание.

Допустим, вы хотите вычислить 107 — 35. Начните с перемещения бусинок, чтобы получилось 107. Переместите одну нижнюю бусину вверх из столбца сотен. Затем переместите одну верхнюю бусину вниз в столбце единиц и две нижние бусинки вверх.

Теперь, чтобы вычесть 35, вы уберете столько бусинок из своей задачи. Вы заметите, что у столбца десятков нет бусинок, которые можно было бы убрать.Вы можете изменить это, переместив одну нижнюю грань вниз в столбце сотен и заменив ее, переместив одну верхнюю грань вниз из столбца десятков и пять нижних граней вверх также в столбце десятков.

У вас еще есть 107 на счетах, просто вы используете другие бусинки. Но, переделав 107, теперь вы можете легко вычесть 35. Чтобы вычесть 35, нажмите три нижних бусинки вниз из столбца десятков и одну верхнюю бусину вверх из столбца единиц.

Теперь, когда вы читаете свои счеты, у вас есть 72 (50 + 20 из столбца десятков и 2 из столбца единиц).Итак, 107 — 35 равно 72.

Резюме урока

Давайте рассмотрим. Счеты похожи на ручной калькулятор со скользящими шариками для представления чисел. На нем есть ряды или столбцы бусинок, которые представляют цифры вашего числа. У вас будут единицы, десятки, сотни, тысячи и так далее.

Китайские счеты имеют столбики из бисера с верхней и нижней частью. В верхней части есть две бусинки, каждая из которых представляет собой 5. Если переместить эти две бусинки вниз, вы получите число 10.В нижней части есть пять бусинок, каждая бусинка представляет собой 1. Если вы переместите три бусинки вверх, вы будете представлять число 3. Вы представляете числа, перемещая бусинки вверх и вниз, чтобы встретиться друг с другом в середине. Чтобы выяснить, какое число показывает счет, просто сложите числа, представленные бусинками. Другая версия абака имеет ряды из десяти бусинок, каждая бусинка представляет 1, а каждая строка представляет различное разрядное значение.

Как производить вычисления с использованием Abacus

Abacus — это древнее вычислительное устройство, которое веками использовалось для выполнения математических вычислений.Счеты бывают двух видов: первая с одной бусинкой на столбец в верхнем ряду и четырьмя бусинами на столбец в нижнем ряду, а вторая — с двумя бусинками на столбец вверху и пятью бусинками на столбец внизу. Дополнительные шарики используются для выполнения шестнадцатеричных вычислений в таких системах, как вес, в которых используется основание 16. Но даже большие счеты можно использовать и для основных десятичных вычислений.

Abacus Basics

Сдвиньте все бусинки к внешнему краю их столбиков, чтобы ни один валик не касался центральной планки.

Используйте каждый столбец на счетах для представления одной цифры в вычисляемом числе, так что крайний правый столбец в нулевом десятичном числе — это столбец единиц, следующий столбец слева — столбец десятков и т. Д.

Сдвиньте одну полоску вверх от нижнего столбца к средней полосе для текущей цифры, чтобы отметить одну, две полоски, чтобы отметить два, и так далее до четырех.

Сдвиньте все четыре бусинки в нижней части вниз и переместите бусинку из верхней части того же столбца к середине, чтобы получилось пять.

Сдвиньте бусинки снизу вверх, удерживая пять на середине, чтобы они представляли шесть — девять.

Сдвиньте все бусинки в ряду от середины, затем сдвиньте одну бусину в ряду слева от середины, чтобы перенести число.

Сложение и вычитание

Сдвиньте бусинки на счетах, чтобы представить первое число в вычислении.

Сдвиньте одну дополнительную бисеринку к медиане в крайнем правом столбце для значения добавляемого числа или сдвиньте одну бисеринку для вычитаемого числа.Например, если единичная цифра первого числа — шесть, а единичная цифра второго числа — два, вы должны добавить два, сдвинув две бусинки вверх в нижнем правом столбце, в результате чего у вас останется пять бусинок и три. Чтобы вычесть два, сдвиньте нижнюю полоску вниз, затем сдвиньте верхнюю полоску от середины, а четыре нижних бусинки обратно к медиане, чтобы получить четыре.

Выполните любой перенос, необходимый для расчета. Например, если добавить от трех до семи для цифры, вы сдвинете две бусинки вверх, обнаружите, что у вас закончились бусинки для скольжения, затем отодвинете все бусинки в текущей строке от медианы, добавив при этом одну бусину в столбец. слева от него.

Выполните обратный перенос или заимствование для вычитания, если вычитаемое число в текущей цифре больше, чем значение цифры в первом числе. Например, чтобы вычесть семь из нуля в столбце, переместите одну бусину в столбце влево от медианы, затем все бусинки в текущем столбце до медианы, затем завершите, вычитая оставшиеся шесть бусинок, как обычно.

Повторите эти действия для каждого столбца, пока не дойдете до крайнего левого столбца.

Использование 100-бусных счётов в элементарной математике

Одним из лучших манипуляторов для первоклассников и второклассников являются простые «школьные» счеты (или 100-бусные счеты), у которых 10 проволок и 10 бусинок на каждой проволоке.

Это не значит, что китайские или японские счеты со специальной системой счета. Я говорю об использовании простых счётов из 100 бусинок для счета и обработки каждой бусинки как 1. Вам не нужно изучать какую-либо из этих сложных систем, которые использовались с различными счетами. Просто считайте, что каждая бусина равна 1 точке.

У вас есть 10 десятков или сотня на ваших счетах, и это имеет большое значение для объяснения десятков и единиц или двухзначного числа детей в детском саду и в первом классе.

Лучше всего, если на счетах будет пять бусинок разного цвета, как на счетах справа. Тогда ребенок без труда узнает 6, 7 и 8 бусинок.

Идеи использования счеты

• Обучающие номера. Сыграйте в простую игру со счетами. Когда наступает ваша очередь, вы произносите число, например 42, и ребенок «набирает» его или показывает на счетах. Затем ребенок называет вам число, и вы показываете его на счетах.Продолжайте так по очереди.


• Более 10 дополнительно. Выберите, например, 6 бусинок на одной проволоке и 8 бисеринок на следующей. Вы можете показать, как пять и пять на этих двух проводах составляют десять, а некоторые остались.


• Узоры на вычитание (и сложение).