Ментальная арифметика: как и зачем решать 10 примеров в секунду
Ментальная арифметика: как и зачем решать 10 примеров в секунду
Умение быстро считать в уме развивает внимание, скорость обработки информации и даже творческое мышление. Дает ли этот навык ребёнку конкурентное преимущество в будущем? Станет ли шагом к успешной жизни или просто отнимет драгоценное время? Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике, рассказывает, в чем польза такого обучения.
Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике
Ментальная арифметика — программа развития умственных и творческих способностей, основанная на системе устного счета. Освоив ее, ребенок сможет решать арифметические задачи в уме всего за несколько секунд. Методика рекомендована для детей от 4 до 12 лет. Однако современные развивающие центры готовы обучать и более взрослых людей, как правило, с одной оговоркой — чем позднее начнешь, тем больше усилий потребуется.
Ментальная арифметика зародилась в Японии в ХVI веке. На начальных этапах обучения используются специальные счеты — абак или соробан. Счеты состоят из рамки, разделительной полосы, вертикальных спиц, верхних («небесных») и нижних («земных») косточек. Одна «небесная» косточка равна пяти «земным». Количество спиц варьируется от 13 до 31. При работе ребенок использует только большой и указательный пальцы. Все движения доводятся до автоматизма. Через некоторое время ребенок совершает вычисления на воображаемом абаке, а задачи решаются с помощью образов.
Формула интеллекта: логика плюс интуиция
Известно, что левое полушарие отвечает за логику, рациональность и анализ, а правое — за образность, целостность, интуицию, фантазию и воображение. Современная система образования уделяет больше внимания точным наукам. Время на танцы, рисование или занятие музыкой выделяется по остаточному принципу. Но даже если родителям удается найти золотую середину, возникает вопрос — как развить взаимосвязь работы обоих полушарий, чтобы максимально раскрыть потенциал ребенка?
Программа обучения метальной арифметики направлена на формирование устойчивых нейронных связей левого и правого полушарий..jpg) По мнению педагогов, именно этот факт помогает людям выбирать наиболее эффективные решения и добиваться успеха в жизни.
По мнению педагогов, именно этот факт помогает людям выбирать наиболее эффективные решения и добиваться успеха в жизни.
Плюсы и минусы ментальной математики
Самый очевидный результат обучения — способность совершать арифметические действия с шестизначными числами за несколько секунд. Но сложно представить, зачем сегодня ребенку может понадобиться этот навык. Как утверждают педагоги по ментальной математике, быстрый счет в уме — это побочный эффект, а не цель. Основная задача обучения — добиться эффекта синергии от синхронной работы обоих полушарий мозга, который превосходит эффект от работы каждого полушария по-отдельности. Тогда вместе с математическими способностями в ребенке будут развиваться:
- усидчивость
- концентрация внимания
- фотографическая память
- воображение
- творческое мышление
- скорость обработки информации
Кроме возрастных ограничений, никаких противопоказаний к занятиям нет. Однако отзывы родителей говорят о том, что не все ученики наблюдают улучшение памяти и концентрации внимания, а у некоторых детей возникают проблемы с решением элементарных задач на логику.
Здесь стоит вспомнить простую истину о том, что каждый ребенок уникален. Менар — это одна из методик развития интеллекта, которая помогает выявить и раскрыть уникальные способности ребенка. Ребенок учится быстро усваивать новую информацию, формулировать мысли и делать выводы. Тем не менее, не стоит пренебрегать традиционными играми — шахматами, головоломками, ребусами. Поэтому, наблюдайте, пробуйте, анализируйте и выбирайте то, что подходит именно вам.
Как проходит обучение
Обучение состоит из 10 уровней, каждый из которых занимает до четырех месяцев. Полный курс длится 2−3 года. Занятия идут по два академических часа один раз в неделю, кроме этого дети должны потратить 15 минут на выполнение домашних заданий. Как правило, у каждого развивающего центра есть онлайн-платформы, которые позволяют более эффективно работать самостоятельно.
Самый главный инструмент — это абак. Также в процесс обучения включают настольные, подвижные игры, просмотр мультфильмов и физминутки.
На первом этапе детей учат складывать и вычитать числа на абаке. В этот период тренируется мелкая моторика, пространственное и логическое мышление. Далее переходят на ментальную карту — картину с изображением абака. И на следующем этапе дети производят арифметические действия с помощью визуализации процесса. Таким образом, уже через год ребенок может делать вычисления в уме.
Как выбрать школу ментальной арифметики?
Результат обучения будет зависеть от трех участников процесса — ребенка, учителя и родителей. Но самое главное — правильно выбрать образовательный центр, где будут преподавать менар. Вот несколько простых правил:
- Запишитесь на пробное занятие. Оцените, насколько комфортно ребенку в новых условиях. Не упустите возможность пообщаться с другими родителями.
- Познакомьтесь с педагогом. Спросите, как готовят преподавателей ментальной арифметики? Контролирует ли головной офис методику преподавания, уровень знаний педагогов, проходят ли преподаватели аттестацию на профпригодность?
- Обратите внимание на количество учеников в группе.
 Только в небольших группах преподаватель может уделить необходимое время каждому ученику. Поэтому в младших группах занимаются 5−7 человек, в старших — 8−10.
Только в небольших группах преподаватель может уделить необходимое время каждому ученику. Поэтому в младших группах занимаются 5−7 человек, в старших — 8−10. - Сделайте анализ рынка. Стоимость обучения в пределах одного региона не может сильно отличаться. Слишком низкая цена может быть показателем недобросовестного подхода к подготовке персонала и разработке методики. Слишком высокая цена может быть связана с издержками, дорогой арендой или рекламой.
Самое главное — чтобы ребенку нравились. Ему должно быть интересно считать, несмотря на то что считать — может быть довольно скучным занятием. Если ребенку нравится, значит, преподаватель смог заинтересовать его. Кроме этого, чтобы оценить преподавателя, обычно спрашивают: через сколько появятся первые результаты? На какие способности влияет обучение? Что делают, чтобы ускорить обучение? Хороший педагог ответит на все вопросы.
Читайте также:
Ну и почерк! Почему детям всё-таки важно учиться красиво писать?
11 полезных советов для родителей от педагога по английскому языку
Зачем детям учить математику?
Фото: GRSI, Ann in the uk, NadyaEugene/Shutterstock. com
com
Ментальная арифметика, ГБОУ Школа № 1797, Москва
Ментальная арифметика – это программа, позволяющая с помощью быстрого устного счёта одновременно развить два полушария головного мозга: левое и правое. Как известно, левое полушарие отвечает у нас за логическое мышление, языковые способности, речь, запоминание фактов, имён, дат. Благодаря левому полушарию мы можем анализировать информацию, обрабатывать её, распознавать символы. Правое полушарие отвечает за интуицию, образное мышление, пространственную ориентацию. Именно из-за нашего «правого помощника» мы чувствуем музыку и чисто поём, понимаем метафоры и сравнения, можем мечтать и фантазировать. Чтобы у вашего сына или дочери развивался весь мозг гармонично, отправьте его на ментальную арифметику.
Благодаря этой методике ваш ребенок будет лучше учиться в школе.
С помощью ментальной арифметики ребенок получит развитие воображения, мышления, памяти. Он сможет решать различные задачи двумя способами: творческим и аналитическим. Из-за своих успехов он поверит в себя, у него повысится самооценка и сформируются лидерские качества. Ментальная арифметика сделает из любого ребенка маленького гения, который в будущем достигнет больших высот.
Основы ментальной арифметики – это упражнения со счетами — абакусом, которые научат вашего ребенка быстро считать в уме. Однако не стоит думать, что быстрый счет — это единственное, что дает методика. Система ментальной арифметики построена таким образом, чтобы развивать оба полушария мозга.
Система ментальной арифметики построена таким образом, чтобы развивать оба полушария мозга.
В основе ментальной арифметики лежит принцип счета.
Принцип счета – самый важный принцип ментальной арифметики. В первый период обучения ребенок сам двигает пальцами обеих рук костяшки, считая сначала простые, а потом сложные арифметические примеры. Затем маленький ученик представляет абакус уже в своем воображении и считает ментально, то есть в уме. Поначалу дети осваивают простые действия: сложение и вычитание. А через год приступают к сложным: умножению и делению. Верится с трудом, но ребенок способен умножать и делить в уме примеры с многозначными числами быстрее калькулятора!
Мы приглашаем детей и их родителей в гости и всегда рады показать вам, как именно проводятся занятия, и рассказать про основы ментальной арифметики для детей.
Дети занимаются в группах. Они набираются в зависимости от возраста, так что ваш ребенок сможет еще и найти новых друзей.
1 день | ||
10. | Знакомство. История возникновения счётных устройств.Теория ментальной арифметики. Цель ментальной арифметики. Какие навыки развивает ментальный счет. | 2 часа |
11.30 – 12.50 | Знакомство с соробаном (абакусом). Постановка рук на соробане (абакусе). Косточки и их значения. Практическое занятие: Работа на соробане (абакусе). Значение цифр на соробане (абакусе). Счёт на соробане (абакусе). Правила сложения и вычитания. Знаки «+», «-» в ментальной арифметике. Одинаковые знаки в ментальной арифметике. Исправление ошибок в ментальной арифметике. Практическая работа. Решение на слух в ментальной арифметике. | 2 часа |
14.00 – 15.20 | Принцип решения примеров на ментальном соробане (абакусе). Практика. Знакомство с упрощенными формулами. Упрощенная формула «-4», «+4» и «-3» и «+3» Практическая работа с использование формулы «-4», «+4» и «-3», «+3». | 2 часа |
15.30 – 16.50 | Упрощенная формула «-2», «+2» и «-1» и «+1» Практическая работа с использование формулы «-2», «+2» и «-1», «+1». | 2 часа |
Всего: | 8 часов | |
2 день | ||
10.00-11.20 | Формулы средней сложности «-7», «+7», «-8», «+8», «-9», «+9». | 2 часа |
11.30 – 12.50 | Принципы решения примеров используя формулы средней сложности «-7», «+7», «-8», «+8», «-9», «+9». | 2 часа |
14.00 – 15.20 | Формулы средней сложности «-4», «+4», «-5», «+5», «-6», «+6». | 2 часа |
15.30 – 16.50 | Принципы решения примеров используя формулы средней сложности «-4», «+4», «-5», «+5», «-6», «+6». | 2 часа |
Всего: | 8 часов | |
3 день | ||
10. | Формулы средней сложности «-1», «+1», «-2», «+2», «-3», «+3». | 2 часа |
11.30 – 12.50 | Принципы решения примеров используя формулы средней сложности «-1», «+1», «-2», «+2», «-3», «+3». | 2 часа |
14.00 – 15.20 | Знакомство со сложными формулами. Сложная формула «-6», «+6», «-7», «+7». | 2 часа |
15.30 – 16.50 | Принципы решения примеров, с использованием сложных формул «-6», «+6», «-7», «+7». | 2 часа |
Всего: | 8 часов | |
4 день | ||
10.00-11.20 | Знакомство со сложными формулами. Сложная формула «-8», «+8», «-9», «+9». | 2 часа |
11.30 – 12.50 | Принципы решения примеров, с использованием сложных формул «-8», «+8», «-9», «+9». | 2 часа |
14.00 – 15.20 | Умножение на абакусе. | 2 часа |
15.30 – 16.50 | Практическая работа. | 2 часа |
Всего: | 8 часов | |
5 день | ||
10.00-11.20 | Деление на абакусе. | 2 часа |
11.30 – 12.50 | Практическая работа. | 2 часа |
14.00 – 15.20 | Закрепление умножения и деления на абакусе. | 2 часа |
15.30 – 16.50 | Практическая работа. Решение на слух. | 2 часа |
Всего: | 8 часов | |
Итого: | 40 ч. | |
Такая разная ментальная арифметика • Абакус+
(Стоит ли доверять ли современным методикам развития ребенка)
Математика — это наука, которая из реального мира берёт какие-то объекты, закономерности и количественные соотношения и, постепенно обобщая их, выводит всё более сложные законы. Конечно же, банальная вычислительная работа с числами не означает знания предмета.
Конечно же, банальная вычислительная работа с числами не означает знания предмета.
Поговорим о Ментальной арифметике, которая на сегодняшний день признана прекрасной развивающей методикой. Однако у многих родителей и учителей не перестают возникать вопросы: насколько полезна эта методика детям?, не разучится ли ребенок считать обычным образом?, не будут ли помехой навыки ментального счета в школе при занятиях традиционной математикой?, полноценно ли развивается мозг ребенка, занимающегося ментальной арифметикой?
В статье мы попытаемся ответить на эти и другие вопросы.
Проанализировав направленность многих существующих школ Ментальной арифметики, мы пришли к выводу, что некоторые из них имеют несколько одностороннюю направленность, хотя и содержат в себе огромный потенциал и развивающий компонент.
К сожалению, не во всех школах ментальной арифметики дети понимают принцип счета, узнают и понимают состав числа. Чаще всего они чисто механически заучивают алгоритмы счета на абакусе, не понимая математической логики в целом.
Чаще всего они чисто механически заучивают алгоритмы счета на абакусе, не понимая математической логики в целом.
Для того, чтобы ученик в начальной школе дошёл до алгоритма сложения столбиком, он должен проделать довольно большой путь: сначала должен научиться складывать/вычитать в пределах десяти, потом делать тоже самое в пределах 20 с переходом через десяток, затем научиться понимать разницу между единицами, десятками и сотнями и так далее. Понимание того, что стоит за числом, как символом, очень важно. И в традиционных курсах ментальной арифметики этому внимание не уделяется, там гонка идет только за скоростью, без глубокого понимания сути.
Именно поэтому, создавая наш курс, мы ставили своей целью полноценное развитие ребенка, а не отдельных его навыков.
Наша программа содержит намного больше, чем обычная «менталка». Поговорим об этом более подробно.
Если говорить о развитии математических навыков и представлений, в первую очередь мы стараемся пояснить детям, откуда взялись алгоритмы счета, которыми апеллирует менталка.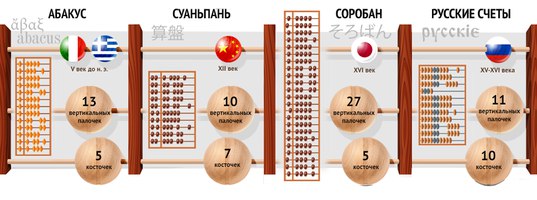
Многие учителя школы прочувствовали на себе, что ребёнок-ментальщик чаще всего не осознает, как на самом деле в реальности происходят вычисления. Поэтому, занимаясь с ребенком практически индивидуально, мы обязательно следим за тем, чтобы ребенок понимал, что и для чего он делает, чтобы его развитие было всесторонним, поэтому включаем в свою программу много дополнительных заданий, таких, которых в традиционном преподавании ментальной арифметике нет.
Именно поэтому в нашем курсе в первую очередь уделяется внимание разбору и пониманию состава числа, и только после этого мы приступаем к математическим операциям на абакусе. Если кто-то интересовался обучающими программами по математике для дошкольников и младших школьников, он наверняка знаком с программой Петерсон Людмилы Георгиевны. В свое время мы были восхищены этой программой и склоняем перед ней голову. Учебники и тетради этого автора прекрасно позволяют ребенку понять логические принципы и математические закономерности. Именно поэтому логика построения нашей программы содержит последовательное вхождение в математику в целом, а не только тренировку навыка счета.
Именно поэтому логика построения нашей программы содержит последовательное вхождение в математику в целом, а не только тренировку навыка счета.
Наша программа дает ребенку возможность полноценно и всесторонне впитать в себя прелесть и красоту математической логики, а в комплексе с ментальной арифметикой помогает развить скорость реакции, сообразительность и умение нестандартно подходить к решению любых задач, умение «видеть» то, что не очевидно. Детей, обучающихся по нашей методике, отличает находчивость в любой ситуации, умение высказать и отстоять свое мнение, уверенность в своих силах, отсутствие страха ошибиться, — все то, что пригодится в любом возрасте для решения любых задач.
Чем же еще отличается наша программа от традиционных? После изучения алгоритмов счета на абакусе наша программа дополнена решением текстовых задач. Причем, не просто задач, а именно задач нестандартных, в которых помимо школьных стандартов нужно иметь еще и внимательность, и творческий подход. Это дает ребенку возможность не только постигать учебный материал наравне со своими сверстниками, но и выходить за границы своего мышления, видеть нестандартные выходы и решения.
Это дает ребенку возможность не только постигать учебный материал наравне со своими сверстниками, но и выходить за границы своего мышления, видеть нестандартные выходы и решения.
В нашей программе нет места пустой «дрессировке» мозга, она не направлена на то, чтобы при виде чисел автоматически представлять в голове счёты и в уме складывать или вычитать эти числа. Мы занимаемся в первую очередь пониманием смысла текстовой задачи и только затем при необходимости применяем ментальный счет.
Именно поэтому наш ученик понимает, что от него хотят, когда решает задачи из традиционного школьного учебника. У него есть представление о том, что нужно сначала разобраться в задаче, и только потом с ней работать.
Некоторые учителя заметили, что дети, занимающиеся традиционной «менталкой», практически всегда в задачах в качестве ответа называют просто одно число. Мы же обучаем детей так, чтобы они давали развернутый ответ, тем самым еще и помогаем учителю школы в развитии речи ребенка.
В отличии от традиционных ментальных школ в наш курс включено понимание «объема» числа. У наших детей есть четкое представление об этом. Наши дошкольники очень хорошо представляют себе физический смысл тысяч, сотен, десятков и т.д. Этому мы уделяем огромное внимание, рассматривая и «перебирая» в руках бусы с разным количеством бусинок, и, представляя количественный признак на других предметах. Именно поэтому для наших детей 52 и 25 – это разные понятия, разные объемы, и есть понимание различия между ними. А вопрос вроде «сколько в сотне десятков?» не вызывает трудностей, как у некоторых детей «ментальных» школ.
В младшем возрасте ребёнку полезно играть в подвижные игры, и чтобы малыш бесконечно не сидел за столом перед счётами в строго определённой позе, в наших занятиях (даже дистанционных) есть упражнения с мячиком, с балансирами, танграммами и головоломками, игры на внимание в кругу, мы прыгаем и веселимся, а не только учим алгоритмы.
Благодаря «синтезу» ментальной арифметики и традиционной математики, который стоит во главе угла в нашей программе, наши дети считают быстрее, становятся более усидчивыми, у них улучшается воображение, совершенствуется развитие мелкой моторики, в целом развивается интеллект. И самое главное – она любят математику!
Расскажем про мелкую моторику. Она очень важна, так как связана с нервной системой, зрением, вниманием, памятью и восприятием ребёнка. Для развития у детей мелкой моторики есть специальные упражнения, которые в первую очередь должны быть разнообразными. Поэтому помимо упражнений на абакусе в наш курс включено множество других упражнений и заданий – это и пальчиковая гимнастика, и массаж пальчиков и ладошек, и лабиринты, и шнуровки, обведение по контуру, лепка из пластилина, раскраски (причем, и правой и левой руками) и многое другое.
Есть мнение, что воображение ребенка, занимающегося «менталкой» развивается однобоко. Действительно, при занятиях ментальной арифметикой в голове необходимо постоянно удерживать образ абакуса, на котором происходят воображаемые вычисления и может показаться, что мысленная фотография абакуса настолько впечатывается в мозг, что её оттуда и трактором не вытащить. Именно для того, чтобы мозг ребенка не «циклился» на одном образе, в наши занятия включены упражнения на развитие памяти, в которых мы предоставляем ребятам для запоминания разнообразные предметы, картинки и цвета, тем самым «разбавляя» образ абакуса и расширяя возможности мозга.
Действительно, при занятиях ментальной арифметикой в голове необходимо постоянно удерживать образ абакуса, на котором происходят воображаемые вычисления и может показаться, что мысленная фотография абакуса настолько впечатывается в мозг, что её оттуда и трактором не вытащить. Именно для того, чтобы мозг ребенка не «циклился» на одном образе, в наши занятия включены упражнения на развитие памяти, в которых мы предоставляем ребятам для запоминания разнообразные предметы, картинки и цвета, тем самым «разбавляя» образ абакуса и расширяя возможности мозга.
А еще есть «задания с продолжением» — это задания, в которых ребенок может сам составить задачу, придумать к ней вопрос – вот и развитие воображения в нашей программе. При этом в таких заданиях мы задействуем образы героев сказок, тем самым, развивая творческое мышление ребенка.
Многие родители на сегодняшний день сильно загружены и доверяют развитие и воспитание своих детей кружкам, детским садам и школе. Именно поэтому нужно с особой тщательностью выбирать для ребенка не только курс развития, а и преподавателя (который должен иметь педагогическое образование) и, как минимум, интересоваться у ребенка тем, что он изучает в детском саду или на развивающем курсе, чтобы понимать, полноценно ли развивается дитя. И, как максимум, заниматься с ребенком, играть с ним, рассказывать сказки, обсуждать героев, говорить о чувствах и ценностях, растить не «счетную машинку», а человека, чтобы после не обвинить учителей, систему образования и мировое правительство, в том, что они загубили талант.
Именно поэтому нужно с особой тщательностью выбирать для ребенка не только курс развития, а и преподавателя (который должен иметь педагогическое образование) и, как минимум, интересоваться у ребенка тем, что он изучает в детском саду или на развивающем курсе, чтобы понимать, полноценно ли развивается дитя. И, как максимум, заниматься с ребенком, играть с ним, рассказывать сказки, обсуждать героев, говорить о чувствах и ценностях, растить не «счетную машинку», а человека, чтобы после не обвинить учителей, систему образования и мировое правительство, в том, что они загубили талант.
Желаем всем удачи!
Л.В.Рябушенко
Ментальная арифметика педагогам | Rich Brain
Ближайшая запись на курс июнь 2020 г.
Мы являемся партнерами Московского педагогического Университета.
Программа ментальная арифметика прошла экспертные заключения
и рекомендована для преподавания в учебных заведениях.

Записаться можно на нашем сайте, сайтах МГПУ или ДПО МОС
Программа 1 уровня Сложение и Вычитание.
День 1. История возникновения счета на Абакусе. Родоначальники и создатели ментальной арифметики. Особенности преподавания в разных школах и отличия методик. Знакомство с Абакусом, цифры, разряды. Простой счет. Отработка движений на абакусе.
Принцип работы на онлайн тренажере по ментальной арифметике.
Простой счет практика. Однозначные двузначные числа.
Основы простого счета, календарно-тематическое планирование простого счета, его особенности с младшими и старшими детьми. Ментальный счет простых чисел.
Знакомство с формулами 5. Принцип работы. Постановка рук при счете. Методические рекомендации для проведения занятий. Практические занятия на онлайн тренажере.
Домашняя работа. Все тренера выполняют домашнюю работу на онлайн тренажере, мы контролируем правильность выполнения.
День 2.
Практическое занятие на абакусе, отработка правил. Особенности ментального счета.
Игры на воображение. Проведение физ. минуток. Способы ментального счета. Особенности ментально счета детей дошкольного возраста, старшего возраста. Как проверять детей на «ментальный счет.
Изучение формул 10 однозначных. Основные движения, принцип работы. Знакомство с тетрадями. Как работать в тетрадях с детьми.
Домашняя работа. Все тренера выполняют домашнюю работу на онлайн тренажере, мы контролируем правильность выполнения.
День 3. Тестирование по пройденным темам. Знакомство с тренажерами на платформе. Особенности тренажеров. Проведение шоу-урока участниками тренинга. Разбор частых вопросов от родителей.
Личность тренера(основные роли и функции) Знакомство с формулами 5+10 однозначными.
Тренировка на платформе. Разбор частых ошибок детей. Создание личных кабинетов тестовых учеников, задание домашних заданий на платформе. Принцип работы разрядов+ формул.
Принцип работы разрядов+ формул.
День 4. Тестирование по пройденным темам. Проверка домашних заданий. Вопрос-ответ. Особенности долгосрочной работы с родителями. Теория и практика двузначных, трехзначных чисел. Методика преподавания двузначных, трехзначных чисел. Знакомство с методическими материалами для преподавания.
После прохождения курса:
-Проводится тестирование, после которого выдается сертификат нашей школы и удостоверение МГПУ.
-Бесплатный доступ на 2 недели к онлайн тренажеру, для тренировок.
-Программа для предоставление в государственное учреждение
-Возможность работать по нашим тетрадям.
-Методические рекомендации.
-Возможность принятия участия в семинарах.
-Поддержка при работе на нашей платформе.
Наши преимущества
Занятия ведет основатель Rich Brain практикующий педагог.
Собственная онлайн платформа, не требующая дополнительных материалов.
Эффективность занятий на онлайн тренажере в 3-5 раз превышает результаты других школ.
Разработанные нами учебники для детей.
Методика проверенная временем, не теория, а практика.
Занятия проходят в Г. Москва, шаговая доступность м. Алма-Атинская, и м. Тульская здание МГПУ
Программа 2 уровня Умножение и деление
Длительность курса 2 недели по 3 часа. Всего 12 часов.
По прохождению курса выдается сертификат нашей школы.
День.1. Легкое изучение таблицы умножения. Особенности обучения детей не знающих таблицу умножения. Календарно-тематическое планирование. Подготовка детей к умножению.
Умножение двузначных на однозначные числа. Умножение трехзначных на однозначные. Двузначных на двузначные числа.
Хитрости 11.
День. 2. Хитрости двузначные. Умножение на числа в заданном диапазоне.
Умножение четырехзначных на однозначные. База 100. Отработка правил на онлайн тренажере.
День. 3. База 50, База 200. Повторение. Промежуточное тестирование по пройденным темам. Домашние задания на онлайн-платформе.
База 50, База 200. Повторение. Промежуточное тестирование по пройденным темам. Домашние задания на онлайн-платформе.
Возведение в квадрат. Секреты возведения в квадрат чисел в диапазоне.
День. 4. Деление Двузначных, Трехзначных, Четырехзначных чисел на однозначное.
Деление на двузначное число. Методика преподавания умножения и деления.
Актуальность ментальной арифметики для развития детей
Современные образовательные программы направлены на обучение детей логическому мышлению, т.е. на усиленный тренинг левого полушария мозга. Правое полушарие, отвечающее за воображение и творческие способности, получает недостаточное развитие, и в результате гармония личности оказывается разрушенной. Между тем, только союз логики и творчества способен сделать человека по-настоящему успешным. Один из эффективных путей равновесного развития обоих полушарий — принципы ментальной арифметики, основанные на использовании обычных косточковых счёт, или абакуса.
Счёты — древнейший калькулятор
Ещё в глубокой древности люди начали использовать различные предметы, чтобы облегчить выполнение подсчётов. Наиболее удачным приспособлением, созданным несколько тысяч лет назад и дошедшим почти в неизменном виде до наших дней, стали обычные счёты, или абакус. Принцип их функционирования очень прост: несколько рядов бусин, перемещаемых на верёвочках, помогают представить любое число в виде комбинации бусин, а также совершать с этим числом простейшие арифметические действия.
Вместо того, чтобы запоминать значки, обозначающие цифры, и их сочетания, ребёнок вначале манипулирует счётными бусинами, а затем переходит к их перемещению в своём воображении, чтобы выполнить тот или иной подсчёт. При этом активно работают оба полушария — и левое, обеспечивающее счёт, и правое, отвечающее за работу воображения. После недолгой тренировки скорость подсчётов в уме возрастает, так как правое полушарие работает быстрее левого. Всё, что нужно сделать, чтобы сложить или вычесть многозначные числа — представить их отложенными на костяшках абакуса и получить готовый ответ.
Всё, что нужно сделать, чтобы сложить или вычесть многозначные числа — представить их отложенными на костяшках абакуса и получить готовый ответ.
Польза ментальной арифметики
По всему миру психологи бьют тревогу: у детей, с дошкольного возраста использующих калькуляторы, компьютеры и другие гаджеты, резко падает воображение. В то же время единственная функция человека, пока что недоступная компьютерной технике — это творчество, создание новых идей, смыслов и проектов.
Только человеческий мозг способен обрабатывать огромные массивы информации, отбирая и соединяя её по едва уловимым признакам. Это качество нередко называют эмпатией или интуицией, но во многих случаях именно так проявляется заложенное в людях творческое начало. Лишённый столь важного умения человек неспособен добиться заметного успеха в любой сфере деятельности, поскольку не сможет создать ничего нового, выйдя за рамки общепринятых процессов. Причём равное развитие должны получить обе стороны ментальной деятельности — и творческие, и логико-аналитические способности.
Ощутимые результаты
Если взрослые люди могут заставить себя упорно трудиться для достижения поставленной цели, то ребёнку важно получить видимый результат как можно скорее. У него недостаёт терпения ждать неделями и месяцами, развивая и оттачивая свои навыки. Именно этим, по мнению многих педагогов, объясняется взрывная популярность книг о Гарри Поттере. Дети, казалось бы, прочно забывшие о том, что существует такой вид досуга, как чтение книг, с энтузиазмом принимались за толстые фолианты произведений Дж. Роулинг.
Доктор психологии К. Поливанова объяснила этот феномен очень просто: дети идентифицировали себя с мальчиком-волшебником, для которого множество проблем решались буквально одним взмахом волшебной палочки. Достаточно взмахнуть ею и прочесть заклинание, чтобы увидеть результат. Сегодня многим детям не хватает именно этого — выполнения действий, которые приводят к быстрому и заметному результату.
Ментальная арифметика является именно таким методом: она ориентирована на быстрое достижение целей. Программа является своеобразной волшебной палочкой, которую могут использовать сами дети, их родители и учителя. Человек, владеющий принципами ментальной арифметики, обретает возможности волшебника. Вы развиваете физические способности, выполняя различные упражнения, но точно так же, специальными комплексами упражнений, следует развивать и мышление.
Программа является своеобразной волшебной палочкой, которую могут использовать сами дети, их родители и учителя. Человек, владеющий принципами ментальной арифметики, обретает возможности волшебника. Вы развиваете физические способности, выполняя различные упражнения, но точно так же, специальными комплексами упражнений, следует развивать и мышление.
Особенности ментальной арифметики
Чем больше вы упражняете мозг, тем легче и быстрее он справляется с новыми задачами. Тренировка заключается в образовании всё большего числа связей между нейронами головного мозга, расположенными в правом и левом полушариях. Рост числа таких связей является обязательным условием ускорения мыслительного процесса, и в результате человек легко справляется с задачами, которые ещё недавно казались ему недостижимо сложными.
Наиболее важно развивать нейронные связи у детей в период между четырьмя и двенадцатью годами. Это самый ответственный этап в жизни человека, который является определяющим для его будущих способностей и возможностей. Занимаясь ментальной арифметикой, дети вначале учатся считать при помощи абакуса, затем — выполнять подсчёты, используя воображаемый абакус. В результате ребёнок получает навыки:
Занимаясь ментальной арифметикой, дети вначале учатся считать при помощи абакуса, затем — выполнять подсчёты, используя воображаемый абакус. В результате ребёнок получает навыки:
- быстрого счёта в уме;
- концентрации внимания на решении определённой задачи;
- творческих способностей, фантазии, воображения;
- умения находить разные пути для решения поставленных задач;
- аналитического мышления, логики, системного подхода к любой проблеме.
Кроме того, существенно укрепляется память, дети получают возможность без усилий запоминать большие массивы цифровой, текстовой и зрительной информации. У малышей к этому прибавляется развитие мелкой моторики пальчиков, что не менее важно для успешного развития интеллектуальных возможностей.
Зачем ребенку ментальная арифметика – советы специалистов из ЮВАО
В последнее время все чаще на улицах и в СМИ встречается реклама курсов ментальной арифметики для детей. С помощью занятий обещают отвлечь их от гаджетов, улучшить успеваемость в школе, развить память и многое другое. Что это за методика и почему она так популярна, рассказали преподаватели ментальной арифметики, работающие в ЮВАО.
С помощью занятий обещают отвлечь их от гаджетов, улучшить успеваемость в школе, развить память и многое другое. Что это за методика и почему она так популярна, рассказали преподаватели ментальной арифметики, работающие в ЮВАО.
ЛУЧШЕ С ПЯТИ ЛЕТ
Счет помогают вести вертикальные счеты абакус (второе название — соробан)/Fotobank
Ментальная арифметика — это методика обучения быстрому устному счету с помощью визуализации математических примеров на вертикальных счетах абакус (второе название — соробан), которые придумали еще до нашей эры.
В Европу ментальная арифметика пришла из Китая и Японии, там она входит в обязательную школьную программу в дополнение к обычной математике.
Начинать занятия рекомендуют с пяти-шести лет, поскольку это лучший возраст для восприятия новой информации и развития одновременно двух полушарий мозга.
— Если к нам приходит дошкольник, сначала мы проверяем его способность понимать числа, затем объясняем принцип работы соробана, учим решать на нем примеры механически, с помощью пальцев, и уже после этого делать то же самое мысленно, представляя соробан в уме.
Чтобы понять, чем отличается привычное нам вычисление в уме от ментальной арифметики, нужно знать алгоритмы вычислений на соробане, — говорит Анна Еременко, преподаватель одного из крупных сетевых центров ментальной арифметики в Текстильщиках.
Решая пример, ребята шевелят пальцами, мысленно передвигая костяшки, и со стороны для многих это выглядит необычно.
Благодаря тому, что в ходе решения примеров задействуются и правое, и левое полушария мозга, у детей развиваются внимание, память, мышление.
Лилия Рябушенко ведет занятия по ментальной арифметике для ребят с ограниченными возможностями здоровья в школе в районе Южнопортовый.
— Ребятам занятия помогают развить мелкую моторику, речь, улучшают память и концентрацию, — говорит она.
НЕ ВОЛШЕБСТВО, А ТРЕНИРОВКА
Те, кто регулярно занимается ментальной арифметикой два раза в неделю по два часа плюс ежедневные занятия дома, уже через пару месяцев могут за считанные секунды решать длинные примеры на сложение и вычитание и поражать родственников своими способностями.
Осваивать ментальную арифметику лучше в детстве/Fotobank
— Те, кто незнаком с методикой, думают, что это волшебство. На самом деле это результат регулярных тренировок, — подчеркивает Анна Еременко. — Надо понимать, что ментальная арифметика ни в коем случае не заменяет математику, хотя и способствует более быстрому освоению материала.
По словам Анны Еременко, школьные уроки направлены в первую очередь на развитие левого полушария, которое отвечает за логику и анализ, а развитие правого полушария, отвечающего за образы, воображение и творчество, отходит на второй план. Поэтому с возрастом осваивать ментальную арифметику становится сложнее.
БЫСТРО СООБРАЖАЕТ И САМА ДЕЛАЕТ УРОКИ
Амина Дейнега из Жулебина занимается ментальной арифметикой два с половиной года. Сложение и вычитание она уже освоила, сейчас изучает умножение. За 10 секунд Амина может в уме умножить, например, 785 на 6.
— Девочка у меня от природы не очень собранная, но благодаря занятиям она научилась концентрироваться, ее не надо усаживать за уроки: все предметы она делает сама.
Ну и по математике в классе она, конечно, лучшая, — говорит мама Амины Елена.
Всего в обучении ментальной арифметике три ступени. После умножения и деления ребята могут освоить примеры со степенями и корнями.
Ментальная арифметика | SkillsYouNeed
Ментальная арифметика — это бесценный математический навык, позволяющий производить вычисления в уме без использования каких-либо инструментов, таких как калькулятор, ручка, бумага или пальцы! Он может пригодиться в бесчисленных повседневных ситуациях, от разработки лучшей сделки с несколькими покупками в супермаркете до расчета, как долго вам нужно будет ждать следующего поезда.
Люди, которым необходимо использовать математику в своей работе, будь то бухгалтерский учет, розничная торговля или инженерное дело, например, часто делают довольно сложные и быстрые оценки в своей голове, чтобы иметь хорошее представление о том, какой будет ответ, прежде чем они приступят к пора сделать более сложный расчет.
Ментальная арифметика также помогает развить настоящее понимание математических методов арифметики, а не просто выполнять вычисления посредством запоминания.
Практика ментальной арифметики может показаться тяжелым трудом, а некоторым людям, которые считают математику сложной, это может даже показаться пугающей перспективой. Но, как и во всем, чем больше вы это делаете, тем легче становится. Эта страница дает вам несколько полезных советов, которые сделают процесс быстрее, проще и намного менее пугающим.
Каждый может научиться ментальной математике! Они не только для математиков.
Умножение чисел на 10, 100 и 1000 и их кратные
Чтобы выполнить простое умножение, вам необходимо иметь базовое представление о разряде . Подробнее об этом читайте на нашей странице Numbers . Здесь следует помнить две вещи:
- Важны нули
- Десятичные точки всегда отделяют целые числа от «битов».

Чтобы мысленно умножить любое число на 10:
Оставьте десятичную точку на месте. В уме переместите все цифры на одну позицию влево и при необходимости добавьте в конец ноль.
24 × 10 = 24,0 × 10 = 240
175 × 10 = 175,0 × 10 = 1750
3,56 × 10 = 35,6
Вы можете перемещать десятичную точку вместо цифр, но только то или другое!
Некоторым людям легче думать о перемещении десятичной точки, чем о перемещении цифр.В приведенном выше примере десятичная точка остается на том же месте, а все цифры сдвигаются влево.
Это то же самое, что и перемещение десятичной точки вправо !
24 × 10 = 24,0 × 10 = 240
175 × 10 = 175,0 × 10 = 1750
3,56 × 10 = 35,6
Чтобы умножить любое число на 100:
Либо
Оставьте десятичную точку на месте. Переместите цифры на два места влево , добавляя при необходимости нули в конце:
845 × 100 = 845. 00 × 100 = 84500
00 × 100 = 84500
37,64 × 100 = 3764
OR
Переместите десятичную запятую на два разряда вправо:
56,734 × 100 = 5673,4
Чтобы умножить любое число на 1000:
Используйте любой из двух методов, как и раньше, и переместите на три позиции :
Переместите цифры влево:
23,476 × 1000 = 23476
Или переместите десятичную точку вправо:
8,45692 × 1000 = 8456,92
Умножение на десятки, сотни и тысячи или более:
Основная идея: если вам нужно умножить число на 200, сначала умножьте на 2, а затем переместите цифры.Вы можете сделать это с любым количеством. Например, если вам нужно что-то умножить на 5000, сначала умножьте свое число на 5, а затем переместите три десятичных разряда.
Количество перемещаемых мест всегда равно количеству нулей.
Например, умножьте 25 на 5000. Это довольно сложно сделать в уме, но весь фокус в том, чтобы разбить это на простые вычисления.
Сначала умножьте 25 на 5:
25 × 5 = 125
Затем переместите цифры на три позиции влево (или десятичную точку на три позиции вправо):
125 × 1000 = 125000.
Деление на 10, 100, 1000 и кратное
Этот процесс точно такой же, как и при умножении, но в обратном порядке.
Чтобы разделить на 10, вы либо
оставьте десятичную точку на месте и переместите цифры на одну позицию вправо,
или
переместите десятичную запятую на одну позицию влево.
За 100 вы перемещаетесь на два места.
За 1000 вы перемещаетесь на три позиции и так далее.
785 ÷ 100 = 7,85
56 ÷ 1000 = 0,056
Помните, что слева от десятичной точки всегда должен стоять ноль, если ваш ответ меньше 1,0
450 ÷ 1000 = 0,450 = 0,45
Вы можете удалить любые нули справа от чисел после десятичной точки. Однако НЕ МОЖЕТ сделать это, если нули стоят перед десятичной точкой или между десятичной точкой и другими числами.
Однако НЕ МОЖЕТ сделать это, если нули стоят перед десятичной точкой или между десятичной точкой и другими числами.
Погружения, кратные десяткам, сотням или тысячам (или более):
Основная идея: если вам нужно разделить на 7000, сначала разделите на 7, а затем переместите цифры на три пробела.
Например, 56 ÷ 7000:
56 ÷ 7 = 8
8 ÷ 1000 = 0,008
Ваш ответ соответствует ожиданиям?
Если вы беспокоитесь, что не помните, двигаете ли вы мысленно свои цифры влево или вправо, взгляните на свой ответ.
Если вы умножаете исходное число на число больше 1, вы ожидаете, что ваш ответ будет больше, чем число, с которого вы начали.
Аналогично, если вы делите на число больше 1, ваш ответ будет меньше. Если это не так, то вы знаете, что ошиблись!
Сложение и вычитание в уме
Так же, как вы это делали с умножением и делением в уме, вы можете изучить некоторые приемы, которые упростят умственное сложение и вычитание.
Как и раньше, эти уловки не связаны с математическим волшебством, это просто случай разбивки задачи на более мелкие части, которые легче решить в уме.
Лучше всего это сделать с помощью нескольких примеров.
Пример 1:Разделение вычитания на сотни, десятки и единицы (или более).
Посчитайте 352 — 13 в уме.
Разделите это на два более простых вычитания: отнять 13 — это то же самое, что отнять 10, а затем отнять 3.
352 — 10 = 342
342 — 3 = 339
Пример 2:
Вы можете применить тот же принцип, что и в примере 1, к более сложному вычитанию:
Посчитайте 4583 — 333 в уме.
Сначала уберите 300, затем 30, затем 3:
4583-300 = 4283
4283-30 = 4253
4253-3 = 4250
Пример 3:
Работа с неудобными числами, близкими к 10:
Посчитайте 77 — 9 в уме.
Убрать 9 — это то же самое, что убрать 10, а затем добавить 1.
77 — 10 = 67
67 + 1 = 68
Пример 4:
Работа с неудобными числами, близкими к 100:
Посчитайте 737 + 96 в уме.
Добавление 96 аналогично сложению 100 с последующим вычитанием 4.
737 + 100 = 837
837 — 4 = 833
Пример 5:
Работа с неудобными числами, близкими к 1000 (или даже больше):
Посчитайте 5372 — 985 в уме.
Этот выглядит даже сложнее, чем другие, но независимо от того, насколько велики задействованные числа, вы все равно можете разбить расчет на простые части.
Вычитание 985 аналогично вычитанию 1000 с последующим добавлением 15 (поскольку 1000–985 = 15).Вы даже можете добавить 15 поэтапно, добавляя 10, а затем добавляя 5.
5372 — 1000 = 4372
4372 + 10 = 4382
4382 + 5 = 4387
Сложение и умножение в голове
Иногда у вас в голове возникает действительно сложный расчет, и это кажется невозможным. Однако, если вы посмотрите на то, как его можно разделить, используя навыки, полученные в примерах выше, что-то действительно сложное может стать намного проще.
Однако, если вы посмотрите на то, как его можно разделить, используя навыки, полученные в примерах выше, что-то действительно сложное может стать намного проще.
Например, посчитайте 97 × 7 в своей голове .
Есть два способа справиться с этим, и вы можете найти один способ проще, чем другой:
Метод 1:
97 совпадает с (100 — 3), поэтому вы можете думать о вычислении как
7 × (100-3)
Это то же самое, что
(7 × 100) — (7 × 3)
Теперь вы заменили сложное умножение двумя простыми умножениями и вычитанием:
7 × 100 = 700
7 × 3 = 21
700 — 21 = 700 — 20 — 1 = 679
Следовательно, 97 × 7 = 679
Метод 2:
97 — это почти 100, поэтому вы можете начать с вычисления 7 × 100 = 700.
Следующий шаг — учесть разницу между 97 и 100, которая составляет 3.
Итак, 7 лотов из 3 — это 21.
700 — 21 = 679
Применение навыков умственной математики к деньгам и процентам
Как вы узнали из приведенных выше примеров, умственные математические навыки сводятся к тому, чтобы разбить задачу на числа, с которыми легко справиться в уме. Иногда нам нужно перевернуть расчет и подумать о нем по-другому.
Иногда нам нужно перевернуть расчет и подумать о нем по-другому.
Два примера, когда вам могут понадобиться ваши умственные математические навыки, — это когда вы имеете дело с деньгами или когда вам нужно вычислить процент, оба из которых часто возникают, когда вы ходите по магазинам.
При работе с деньгами можно округлить сумму до ближайшего целого фунта, а затем обработать пенни отдельно. Вы часто видите цены, отмеченные таким образом, чтобы заставить вас думать, что они дешевле, чем они есть на самом деле. Например, 24,99 фунта стерлингов — это всего лишь один пенни от 25 фунтов стерлингов, но продавец хочет, чтобы вы подумали, что это ближе к 24 фунтам стерлингов.Когда вы делаете мысленные математические вычисления, иметь дело с 25 фунтами стерлингов намного проще, чем с 24,99 фунтами стерлингов.
Полезный мысленный прием для вычисления процентов — это помнить, что они обратимы, поэтому 16% от 25 равно 25% от 16. Неизменно одно из них будет намного легче вычислить в уме… попробуйте!
Заключение
Ментальная арифметика может показаться довольно пугающей, но со временем вы сможете использовать эти приемы ментальной математики, чтобы разбить сложную задачу на более мелкие части, над которыми легче думать. Здесь нет никакого волшебства, просто нужно взглянуть на проблему по-другому.
Здесь нет никакого волшебства, просто нужно взглянуть на проблему по-другому.
Дополнительная литература по навыкам, которые вам нужны
Основы счета
Часть необходимых навыков Руководство по счету
Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами. Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.
Если вы хотите освежить в памяти основы или помочь своим детям в учебе, эта книга для вас.
Сложить мысленно целые числа — Полный курс арифметики
435 + 461 = 896
Сначала сложите сотни, затем десятки, затем единицы.
Теперь мы видим фундаментальный принцип всех мысленных вычислений:
Считайте слева направо, как вы читаете.
Последнее число, которое вы скажете, — это ответ
Пример 5. Счет по десяткам. 30 + 24 = 54.
Счет по десяткам. 30 + 24 = 54.
Вот другие примеры:
20 + 16 = 36
40 + 38 = 78
40 + 62 = 102
40 + 82 = 122
90 + 73 = 163
Пример 6. 43 + 25
Сначала сложите десятки, затем единицы.Скажите
«Шестьдесят —
43 + 25
— восемь ».
Или, можно сказать,
«43 плюс 20 равно 63, плюс 5 равно 68».
Скажем: «150 плюс 7 равно 157.»
Скажите только: «50 плюс 14 — 64».
Искусство мысленного расчета — говорить как можно меньше. Последнее число, которое вы скажете, и есть ответ.
«170 плюс 11 равно 181.»
Пример 10. 23 + 32 + 25 + 12
Сначала сложите все десятки, затем добавьте единицы. Добавляя каждое место, называйте частичную сумму. Скажите
Последнее число, которое вы скажете, — это вся сумма.
| Пример 11. | 34 + 25 + 32 |
| «50, 80, 89, 91 .« | |
Пример 12. 653 + 224
Сначала сложите сотни, затем десятки, затем единицы. Снова произнесите каждую частичную сумму:
653 + 224
Скажем,
«800, 870, 877 .»
Пример 13. Три трека на компакт-диске имеют следующие времена:
10:34
6:25
8:07
Сколько всего времени?
10:34 означает 10 минут 34 секунды.60 секунд = 1 минута.
(Следовательно, 72 секунды = 1 минута 12 секунд. 1:12.)
Техника. Начните с минут и сосчитайте:
«16 плюс 8 — это 24 минуты».
Теперь прибавьте секунды.
«24:59 плюс 7 равно 24: 66. «
Общее время 25 минут 6 секунд.
На этом этапе, пожалуйста, «переверните» страницу и выполните несколько задач .
или
Перейти к разделу 2:
Сложите мысленно, округлив
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Месяц знаний математики — Ментальная математика
Навигация по календарю
Быстрее, какой квадрат 347? А как насчет квадрата 721? Не тянись за калькулятором! Если вы Артур Бенджамин, вы можете сделать это в уме:
Да, такое видео-перформанс легко было бы сфальсифицировать. Но в этом нет ничего фальшивого. Действительно, профессор Бенджамин наслаждается обучением методам, лежащим в основе его удивительных достижений в области арифметики. Если вам нужно больше убедить в подлинности его сил, прежде чем двигаться дальше, перейдите к видео TED в следующем разделе. Но если вы хотите научиться некоторым невероятно простым трюкам для выполнения мысленных вычислений, видео ниже — хорошее место для начала.
Теперь, когда вы знаете некоторые основы, оттачивайте свои навыки, проверяя их на своих друзьях. Или подумайте о проблемах ниже …
Вот более длинная и убедительная демонстрация навыков профессора Бенджамина (для всех, кто сомневается в его способностях или просто хочет увидеть больше):
С правильным мышлением можно приручить и использовать арифметические модели.Попробуйте свои силы в решении этих задач, поставленных профессором Бенджамином:
- Выберите число от 1 до 70, а затем разделите его на 7. (Я буду любезен и позволю вам воспользоваться калькулятором, но вам понадобится калькулятор, у которого не менее семи знаков после запятой.) Если ваша сумма равна целому число (то есть без цифр после десятичной точки) снова разделите ответ на 7. Есть ли где-нибудь после десятичной точки 1? Я предполагаю, что число после 1 будет 4. Я прав? Теперь сложите первые шесть цифр после десятичной точки, и вы обнаружите, что ответ — 27.
- Выберите ваше любимое число от 1 до 100. Удвойте его, затем добавьте 5. Теперь умножьте на 50, затем добавьте 1,763. Если у вас уже был день рождения в 2014 году: с днем рождения и прибавьте 1 к общей сумме. Вычтите год своего рождения. Ваш ответ начинается с вашего любимого числа, за которым следует ваш возраст. Почему это работает?
- Выберите четырехзначное число, каждая из которых отличается. Перемешайте цифры, чтобы создать новый номер. (Например, если ваше первое число 2357, второе число может быть 7325.) Вычтите меньшее число из большего и сложите цифры полученного числа. Если ваша сумма одна цифра, дальше не идите. Если ваша сумма представляет собой двузначное число, сложите две цифры вместе. Я предполагаю, что ответ — 9. Я прав?
- В приведенном выше видео TED, начиная с 5:50, профессор Бенджамин просит своих испытуемых умножить число 8 649 на любое трехзначное число. Затем он просит их зачитать все цифры ответа, кроме одной, в любом порядке. Он продолжает говорить им цифру, на которой они остановились.Как он это делает?
Математика, стоящая за вышеупомянутыми задачами и за ментальной арифметикой, на самом деле является простой алгеброй. В задачах-испытаниях алгебра открывает то, что поначалу могло показаться загадочным. Для ментальной математики алгебра часто бывает простой в принципе, но чтобы овладеть ею, нужна практика!
Ответы на (и стоящую за ними алгебру) первые три задачи, приведенные выше, можно найти в статье Ta Da из New York Times (декабрь.30, 2009).
Ответ на последнюю задачу потрясающе прост и основан на хорошо известном факте, что число кратно девяти именно тогда, когда сумма его цифр кратна девяти. (Найдите здесь объяснение.) Обладая этим фактом, профессор Бенджамин впервые заметил, что число 8 649 кратно девяти (так как сумма его цифр равна 27). При умножении на трехзначное число (или на на любое целое число !) Результат все равно будет кратным девяти. Следовательно, сумма цифр в ответе будет кратна девяти.Когда испытуемые показывают все цифры, кроме одной, профессор Бенджамин быстро определяет значение недостающей цифры. Вы можете услышать, как профессор Бенджамин объясняет это (и дает некоторые советы и предостережения), начиная с момента времени 40:50 на видео здесь.
Здесь можно найти еще несколько приемов, основанных на том же принципе. Глава 14 книги Мартина Гарднера «Неожиданное зависание и другие математические отклонения » дает обширный обзор многих тестов на делимость.Любой вводный учебник по теории чисел углубится в еще более подробную информацию.
Хотя быстрое умственное вычисление требует практики, основные принципы, такие как изложенные профессором Бенджамином во втором видео, служат основой. Одним из многих преимуществ такого изучения является осознание того, что в отличие от стандартных карандашных и бумажных методов сложения и умножения, мысленные вычисления обычно приводят вас к нахождению цифр в ответе слева направо, а не справа налево.Это означает, что если вы бросите курить до того, как закончите, у вас есть хотя бы приблизительный ответ! Обратите внимание, что в большом финале видео TED, где пятизначное число возведено в квадрат, первое, что записывает профессор Бенджамин, — это 3, и он знает, что ответ — 3 миллиарда (и что-то в этом роде).
Для тех, кто желает поднять свои умственные математические навыки на новый уровень, книга Артура Бенджамина и Майкла Шермера « Секреты умственной математики: Руководство математика по вычислению молний и удивительным математическим трюкам » (Crown, 2006) отличный ресурс.
(PDF) Ментальная арифметика и использование стратегии с задачами с косвенными числами до ста
МЕНТАЛЬНАЯ АРИФМЕТИКА И ИСПОЛЬЗОВАНИЕ СТРАТЕГИИ 105
Барнард, Ю. Ф., и Сандберг, Дж. А. С. (1988). Применение идей искусственного интеллекта в программе CA1 для решения математических задач «открыть
предложений» в начальной школе. Педагогическая наука, 17, 263-276.
Баруди, А. Дж. (1987). Детское математическое мышление-развивающая основа для дошкольного, начального.и
учителя специального образования. Нью-Йорк: издательство Teachers College Press.
Баруди, А. Дж., И Гинзбург, Х. П. (1986). Связь между начальными осмысленными и механическими знаниями
арифметики. В J. Hiebert (ред.), Концептуальные и процедурные знания: случай математики (стр. 75-1 12).
Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум.
Beentjes, J. W. J., & Jonker, V. H. (1987). Несогласованность в стратегиях сложения и вычитания.Журнал
Э.р. экспериментального образования, 56,4-и ‘.
Beishuizen, M. (1993). Психологические стратегии и материалы или модели для сложения и вычитания до 100 на голландском языке
вторых классов. Журнал исследований в области математического образования, 24,294-323.
Beishuizen, M., Felix, E., & Beishuizen, J. J. (1990). Генетическая модель для обучения навыкам сложения и вычитания
в адаптивной компьютерной программе.В J. M. Pieters, K. Breuer, & P. R. J. Simons (Eds.), Learning
environment-Contributions from Dutch and German Research (p. 15 1-161). Берлин: Springer Verlag.
Beishuizen, M., Van Mulken, F., & Van Putten, C.M. (1993, сентябрь). Ментальная арифметика и стратегическое действие
на сложение и вычитание до ста. Доклад на 5-й конференции EARL1, Экс-ан-Прованс, Франция.
Bruins, R., & Lufting, R.(1986). Kun je rekenen op je method? [Можете ли вы рассчитывать на свою книгу по математике?].
(Неопубликованная кандидатская диссертация). Гронинген: Университет Гронингена, Нидерланды.
Плотник, Th.I? (1985). Учимся складывать и вычитать: упражнение в решении проблем. В Е. А. Сильвере (ред.),
Преподавание и обучение решению математических задач — множественные исследовательские перспективы (стр. 1740). Хиллсдейл, Нью-Джерси:
Лоуренс Эрлбаум.
Карпентер, Т. П. и Мозер, Дж. М. (1984). Освоение концепций сложения и вычитания в классах с первого
до третьего. Журнал исследований в области математического образования, IS, 179-202.
Кобб П. (1995). Культурные инструменты и изучение математики: тематическое исследование. Журнал исследований в области математики
Education, 26, 362-385.
Cobb, P., Gravemeijer, K., Yackel, E., McClain, K. & Whitenack, J.(1995, сентябрь). Математизация и
символизация: Возникновение цепочек значений в одном классе первого класса. Доклад на 6-й конференции EARL1
, Неймеген, Нидерланды.
Damen, S., & Huntink, M. (1989). Hoofdrekenen in handelingspsychologisch Perspectief. [Ментальная арифметика из
с точки зрения психологии действия.] (Неопубликованная магистерская диссертация). Лейден: Лейденский университет,
Нидерланды.
Дебойз, М., и Питт, Э. (1995). Направления развития начальной математики. Белфаст: The Blackstaff Press.
Фройденталь, Х. (1991). Возвращаясь к математическому образованию. Китайские лекции. Дордрехт, Нидерланды: Kluwer.
Фусон, К. К. (1990). Концептуальные структуры для многозначных чисел: значение для обучения и преподавания
многозначное сложение, вычитание и разрядные значения. Познавательные и обучающие, 7,343403.
Фусон, К. К. (1992). Исследование сложения и вычитания целых чисел. В Д. А. Гроусе (ред.), Справочник
исследований по преподаванию и обучению математике (стр. 243-275). Нью-Йорк: Макмиллан.
Фусон, К. К., Ричардс, Дж. И., и Брайарс, Д. Дж. (1982). Приобретение и разработка последовательности цифровых слов.
В C. 1. Брейнерд (ред.), Прогресс в когнитивном развитии-Детское логическое и математическое познание.Vol. I,
(стр. 33-92). Нью-Йорк: Спрингер.
Гир, Дж. П. Ван де (1988). Анализируйте van kategorische gegevens. [Анализ категориальных данных.] Девентер,
Нидерланды: VanLoghum Slaterus.
Гифи А. (1990). Нелинейный многомерный анализ. Чичестер: Вайли.
Гравемейер, К. П. Э. (1994). Развитие реалистичного математического образования. Докторская диссертация, Утрехтский университет.
Утрехт, Нидерланды: Институт Фройденталя.
Харскэмп, Э. Г., и Сухре, К. (1995). Хоофдрекенен в специальном onderwtjs-Eindverslag SVO-project 92081.
[Ментальная арифметика в специальном образовании — Заключительный отчет, SVO project 920811. Гронинген, Нидерланды:
GION.
Хедрен Р. (1995, октябрь). Как думают ученики, когда им разрешают разрабатывать свои собственные методы расчета.
Доклад на Европейской исследовательской конференции по психологии математического образования (ERCME),
Osnabriick, Германия.
Хейден, М. К. Ван дер (1993). Consistentie van aanpakgedrag-Een schemediagnostisch onderzoek naar acht
aspecten van hoofdrekenen. [Последовательность подхода к поведению — исследование процесса оценки восьми
аспектов ментальной арифметики.] Докторская диссертация, Лейденский университет. Лиссе, Нидерланды: Swets & Zeitlinger.
Хейден, М. К. Ван дер (1994). Подход Выготского к исследованию умственного сложения и вычитания до
сотен: удобная арифметика для учеников начальной школы.В J. E. H. Van Luit (Ed.), Исследования в области обучения и обучения математике
в детском саду и начальной школе (стр. 108-124). Doetinchem, Нидерланды:
Graviant.
Хоуп, Дж. А., и Шерилл, Дж. М. (1987). Характеристики неквалифицированных и опытных ментальных калькуляторов. Журнал для
Исследования в области математического образования, IS, 98-111.
Батарея когнитивных тестов для ментальной арифметики (CAB-AR)
Шатил Э (2013).Улучшают ли комбинированные когнитивные тренировки и тренировки физической активности когнитивные способности больше, чем по отдельности? Рандомизированное контролируемое исследование с четырьмя условиями среди здоровых пожилых людей. Фронт. Aging Neurosci. 5: 8. DOI: 10.3389 / fnagi.2013.00008.Korczyn AD, Peretz C, Aharonson V, et al. — Компьютерные когнитивные тренировки с CogniFit улучшили когнитивные способности по сравнению с классическими компьютерными играми: проспективное, рандомизированное, двойное слепое исследование с участием пожилых людей. Болезнь Альцгеймера и слабоумие: Журнал Ассоциации Альцгеймера, 2007 г .; 3 (3): S171.Шатил Э., Корчин А.Д., Перец С. и др. — Улучшение когнитивных функций у пожилых людей с помощью компьютеризированной когнитивной тренировки — Alzheimer’s & Dementia: The Journal of the Alzheimer’s Association 2008; 4 (4): T492, Lubrini, G., Periáñez, J.A., & Ríos-Lago, M. (2009). Introducción a la Estimulaciónognitiva y la rehabilitationación neuropsicológica. En Estimulación когнитивная y реабилитация нейропсикологика (стр.13). Rambla del Poblenou 156, 08018 Барселона: От редакции UOC.cuatro (4): T492.Verghese J, J Mahoney, Ambrosio AF, Wang C, Holtzer R. — Эффект когнитивной реабилитации в условиях оседлого образа жизни — J Gerontol A Biol Sci Med Sci. 2010 декабрь; 65 (12): 1338-43. Эвелин Шатил, Ярослава Микулецка, Франческо Беллотти, Владимир Бурес — Когнитивная тренировка на основе телевидения улучшает рабочую память и исполнительную функцию — PLoS ONE 3 июля 2014 г. 10.1371 / journal.pone.0101472. Gard T, Hölzel BK, Lazar SW. Потенциальные эффекты медитации на когнитивное снижение, связанное с возрастом: систематический обзор.Ann N Y Acad Sci. 2014 Янв; 1307: 89-103. DOI: 10.1111 / ньяс.12348. 2. Voss MW et al. Пластичность мозговых сетей в рандомизированном интервенционном исследовании тренировок с упражнениями у пожилых людей. Front Aging Neurosci. 26 августа 2010 г .; 2. pii: 32. doi: 10.3389 / fnagi.2010.00032.
Обучение детей мысленному счету
Эта публикация была адаптирована из «Стратегии обучения ментальным вычислениям — руководство для учителей на первом и втором ключевых этапах», выпущенного в 1999 г. Национальной стратегией счисления и Управлением по квалификациям и учебным программам (ныне QCDA).Его общая цель — помочь учителям в планировании:
• перечисление числовых фактов, которые учащиеся должны быстро запомнить
• определение ожиданий в отношении типов вычислений, которые учащиеся должны уметь мысленно выполнять
• определение мысленных методов, которым можно обучить учащихся, чтобы помочь им точно и эффективно
• предлагая ряд подходящих занятий в классе и ресурсов, чтобы помочь студентам понять и практиковать методы расчета.
Четыре главы обложки буклета:
Глава 1. Развитие навыков мысленных вычислений
Здесь описывается прогресс в количестве фактов, которые учащиеся должны извлечь и вспомнить, вычисления, которые они должны выполнять мысленно, и диапазон стратегий или методов вычислений, которые они могут использовать.
Глава 2. Принципы обучения мысленному расчету
Это способствует широкому толкованию мысленного расчета и определяет принципы, лежащие в основе обучения: например, побуждение детей делиться своими умственными методами, выбирать эффективные стратегии и использовать неформальные записи для отслеживания информации, необходимой им при расчетах.Также рассматривается роль тестов и опросов.
Глава 3. Стратегии сложения и вычитания
В нем изложены основные стратегии мысленного сложения и вычитания. В нем описываются действия, способствующие обучению этим стратегиям и типичным проблемам.
Глава 4. Стратегии умножения и деления
Здесь изложены основные стратегии умножения и деления в уме. Опять же, в нем описываются действия в поддержку обучения этим стратегиям и типичным проблемам.
В чем разница между арифметикой и математикой?
В чем разница между арифметикой и математикой? Мой любимый быстрый ответ:
Арифметика относится к математике так же, как орфография к письму.
Словарные определения этих двух частей обучения:
арифметика
(1) раздел математики, который занимается сложением, вычитанием, умножением и делением,
(2) использование чисел в вычислениях
математика
(1) изучение отношений между числами, формами и величинами,
(2) он использует знаки, символы и доказательства и включает арифметику, алгебру, исчисление, геометрию и тригонометрию.
Самая очевидная разница в том, что арифметика — это все о числах, а математика — о теории. В колледже я хорошо помню, как Линус Полинг читал гостевую лекцию, и после того, как один студент нацарапал теоретическую математику на трех классных досках, поднял руку и указал, что на одном из предыдущих шагов было неверно умножено 7 на 8. Полингс ответил: «О, цифры — это просто заполнители концепции». И он просто отмахнулся от того факта, что числовое заключение явно не было точным.Так вот, это было в шестидесятые годы, до того, как в изобилии появился доступ к калькуляторам и компьютерам, поэтому его точка зрения еще более актуальна сегодня. Изучите теорию математики, и калькуляторы и компьютеры помогут вам в точности. Тем не менее, очень важно подчеркнуть, что калькуляторы занимают свое место в образовании детей, но не исключают их понимание материала собственным мозгом.
У меня есть друг, который изучал математику в Северо-Западном университете, настоящий гений математики с планами на будущее в области теоретической математики.До того, как однажды летом он открыл для себя бизнес и то, как хорошо он мог думать на ногах. Он мог выполнять сложные арифметические операции в своей голове быстрее, чем кто-либо другой, и благодаря своим продвинутым способностям решения задач у него был уникальный образ мышления. Сейчас он владеет 21 магазином, имеет более 400 сотрудников и путешествует по миру, ведя бизнес на нескольких языках с переводчиками и заключая сделки благодаря своей необычайной способности быстро и точно манипулировать числами в своей голове. Его независимость от калькуляторов делает его таким успешным бизнесменом, каким он и является.
Конечно, и арифметика, и математика абстрактны. В книге «Дзен и искусство ухода за мотоциклами» есть отрывок, в котором отец и его 9-летний сын путешествуют по пересеченной местности на мотоцикле, и, проезжая страну бесплодных земель, отец рассказывает своему сыну о призраках. Затем его сын спрашивает отца, верит ли он, отец, в призраков. Отец отвечает резко и быстро: Конечно, нет! Затем он думает об этом и объясняет своему сыну, что, возможно, он ДЕЙСТВИТЕЛЬНО верит в призраков, потому что он верит в систему счисления, а это привидение.Призрак неконкретен, его нельзя коснуться или почувствовать, нет веса, нет массы. Что такое числа? Это символы со смыслом, и для некоторых связь символов с фактическим процессом подсчета очень абстрактна. Когда мы смотрим на древнеегипетские числа, они становятся для нас бессмысленными символами, если мы не уделили время изучению и связыванию символа с его предполагаемым значением. (Чтобы узнать о хорошей истории математики, посетите http://www-history.mcs.st-and.ac.uk/~history/Indexes/HistoryTopics.html)
И, кроме того, есть мой собственный опыт с арифметикой, которую я мог делать в начальной школе, не очень быстро, но я всегда мог это делать. Я не взбодрился до алгебры для меня, ЭТО было интересно и становилось все более и более интересным по мере моего обучения. Но арифметика всегда преследовала меня как в личной, так и в профессиональной жизни. В моей личной жизни друзья всегда давали мне чек в ресторанах, чтобы складывать и поровну делить между нами, тьфу, это было утомительно, и они просто не понимали, что числа — не мое.В профессиональном плане я стоял перед классом и делал ужасные арифметические ошибки при выполнении сложных математических уравнений, но, слава богу Линусу Полингу, я не относился к этим ошибкам слишком серьезно. Людям трудно понять, что вы учитель математики, но на самом деле вас не слишком заботят числа. Я нахожу увлекательными решение задач и математические теории.
Проведя большую часть своей жизни, преподавая математику в средней школе, было обидно услышать, как мой дядя сказал, что то, что я преподаю, не является настоящей математикой. Его мир преподавал математику физики элементарных частиц продвинутым аспирантам Стэнфордского университета.Лишь горстка людей в мире понимала статьи, которые он писал. Его определение арифметики состоит в том, что она структурирована и что математика не в его уме, счет с помощью исчисления — это арифметика. Теоретическая математика в его статьях была для меня тарабарщиной, а для него — символической прозой, соединяющей математику и естественные науки. С его точки зрения, пока вы не дойдете до продвинутой физики, математика не будет настоящей математикой. Перспектива — это все.
В заключение, арифметика использует числа, а математика использует переменные. Каждая дисциплина имеет свои собственные сложности и мыслительные процессы.
Лауреат Нобелевской премии по химии
Автор писал автобиографически, борясь с философскими вопросами, касающимися сравнения романтического образования и классического образования чувств / эмоций с технологией / рациональным мышлением.
Компоненты ядра атома
2004-2021 Иллана Вайнтрауб, MathMedia Educational Software, Inc. Все права защищены.
Эта работа находится под лицензией Creative Commons License. .


 00-11.20
00-11.20.jpg)
 00 -11.20
00 -11.20